这个问题首先可以从一元函数的微分入手。

首先是高阶无穷小的定义：

上图是高阶无穷小的来历。

微分定义中出现了高阶无穷小。

以上证明过程可以清晰看到微分中高阶无穷小出现的原因。首先是根据导数的定义得出a,这个a是肯定会随着Δx趋于0而趋于0的，因为Δy/Δx就是导数的定义，而当Δx趋于0的时候，导数得到精确值f'(x0)，所以a是Δx趋于0时候的无穷小，a再乘以Δx得到aΔx，当然就是Δx趋于0时的高阶无穷小。

以上是极限的定义。

以上是Δy和dy是等价无穷小的证明，所以两者在Δx趋于0时可以相互替代。

上图是Δy和dy的几何意义。对于x轴上固定两点x和x+Δx，Δy表示的是曲线上相对应两点的高度变化，也就是函数值的变化；dy表示的是切线上相对应两点的高度变化。很明显，当Δx趋于0时，两者趋于一致。高阶无穷小就是曲线上变化的高度减去切线上变化的高度Δy-dy。

下面是多元函数的情况。

上图证明过程中，通过多元函数的连续定义，引入了无穷小epsilon1。为了搞清楚这个问题，首先看多元函数的极限定义：

然后是多元函数连续性定义：

与一元函数连续性定义对比：

上图中出现了epsilon。与图1对比，f(x)就是

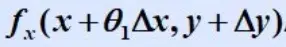
，而f(x0)就是

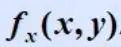
图4中的epsilon肯定会随着x趋于x0而趋于0，这一点很容易由下图的连续函数几何意义看出来：

上图中的Δy就是f(x)-f(x0)。很明显，当Δx趋于0时，Δy也趋于0。

而对于多元函数来说，这个Δx就是下图中的PP0,也就是图1中的epsilon1。很明显，这个epsilon1就相当于图0中的a，而PP0也相当于图0中的Δx，所以图1中的epsilon1会随着PP0(也就是p)趋于0而趋于0。

上图的目的正是为了证明全增量Δz与全微分dz之间的差距

是图2中

的高阶无穷小。

全增量Δz与全微分dz的几何意义如上图。由于

从切平面的方程可以看出，由于z-z0就是dz，x-x0就是dx，y-y0就是dy。

如上图所示，假设A点坐标是（x,y）,B点坐标是

则由这两点在xoy平面向上作两条垂线（这里过A点的垂线与曲面的交点就是M），与切平面交点之间的高度差就是全微分

，而与曲面两个交点之间的高度差就是全增量