数量积不会做？重要方法都在这！投影+极化恒等式+拆解 | 神奇小猪

数量积计算技巧：

一、关于极化恒等式：

题1：

假设M点为中点，利用极化恒等式可以得出PM方-AM方，而AM放在三角形AOB中可以求得并且是一个固定的值，题目问PA'PB最小值实际就是问PM的最小值。

极化恒等式题型：底边固定，求中线长度的取值范围。

题2:

本题中，由于题目中给的不是共起点，先转化为共起点。即AB'AC=4,

FB'FC=-1

假设AE=EF=FD=x,BD=DC=y

根据题目可列：（3x)方-y方=4

x方-y方=-1

所以可以解得：x方=5/8

y方=13/8

二、拆解法：适用于两个向量“横七竖八”

题3：

本题既无法用共起点极化恒等式，也无法用投影角度也不好求，这时题目应用拆解法去求。

▲ABC是等边三角形，且长度也给（角度也知道），题目中的相乘的向量可以以AB、AC为基底来表示。所以实际就是关于基底的运算。

三、如何选用基底 --选基底原则：

1.向多边形的边上分解

2.往圆心分解AB=OB-OA

3.沿直角边分解OD=OA+AD

题4：

本题属于在⚪内的拆解向量

往圆心分解

不取1是因为要满足A、B、C三点构成三角形

题5：

毫无意外，共起点，妥妥的极化恒等式方法

AB长度也知道，自己标圆心，题目中问PA'PB最小值实际就是找OP最小值，当然就是垂直于弦长的时候最小。

把OP放到三角形COD中去求，三线合一，所以可以求出OPmin=根号3

题6：

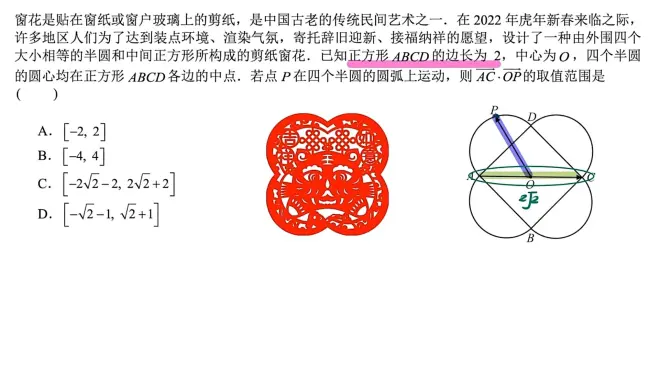
（1）根据有一个向量固定，可知要用投影法

（2）最长相切时：

（3）算最大的投影长度：

因为最大长度为2根号2+2的只有C，选它！