基于Optistruct的SCARA机械臂的拓补优化及设计
几年前写的一个东西,正好碰见最近有人问这个,就放上来
4轴SCARA机器人的结构,觉得第二个连杆可以进行一个优化分析进行轻量化,于是创建了一个简化的模型进行了拓补优化分析,并完成最终三维设计。如下:
一、建模
按照某外资品牌的样本(网上可以自由下载),获得其杆长及其他基本尺寸,依
据此数据进行三维建模:
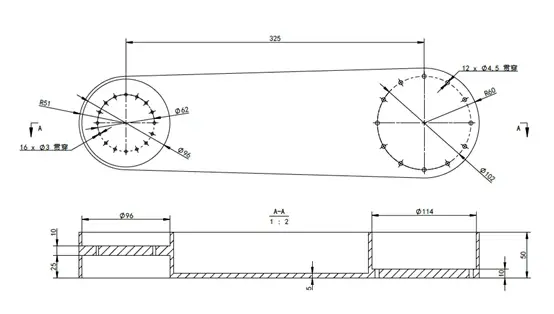
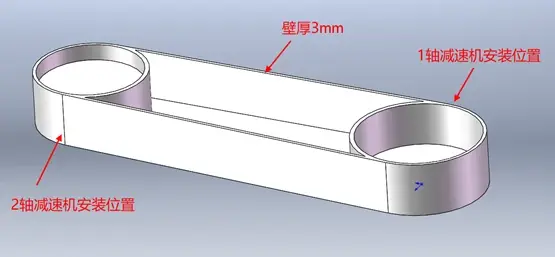
注意:1考虑到机器人外观及功能,上面创建的三维在优化分析中是不能去除材料的,也就是说上面的三维是非设计区域
2. 为什么壁厚是3mm?这个要从工艺的角度来考虑,一般机械臂都为铸造,而铸造常用的工艺用沙铸、重力、高压等。3mm壁厚只能是压铸,如果是沙铸或是重力,壁厚很难做到3mm。
二、 将三维导入hypermesh并划分网格
紫色部分就是上面创建的三维,橙色部分是在hm中生成的,网格尺寸为3mm,3mm其实偏大,不过减小单元尺寸的话,计算量会增加很多,实际设计中,肯定要减小这个单元尺寸
三、 定义材料及属性
n 材料采用铸铝A356(国内牌号ZL101A),E=70000,Nu=0.33
n 定义属性,这里就要注意了,要定义两个属性,其中一个属性赋予非设计区域,一个属性赋予设计区域,虽然这两个属性完全一样,没有任何区别
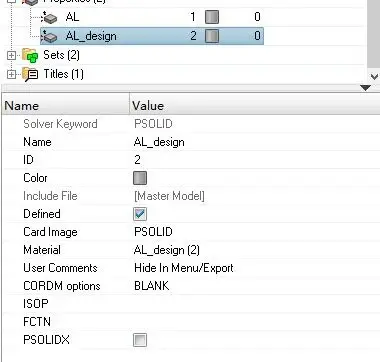
四、 创建工况
1. 边界条件:固定1轴减速机安装面

2. 依据机器人的实际工作情况,创建两种工况:(1)1轴旋转,命名为L1 (2)3轴上下运动,命名为L2
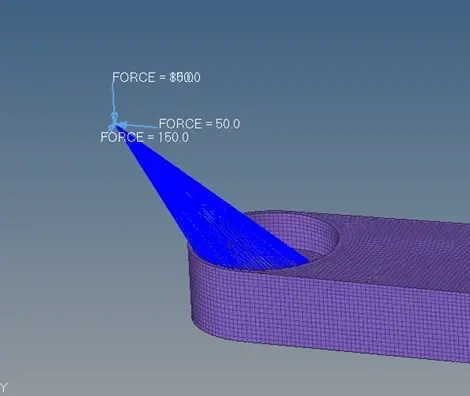
力的大小依据机器人3/4轴的重量及1轴大致的旋转速度而定
最终模型如下图所示:

五、优化分析
首先回忆下优化的三要素:设计变量、约束、目标
1. 定义设计变量


创建好设计变量后,还需要对设计变量进行一定的设置,不然就算优化出来,结果也是没用的

定义最小成员尺寸,也就是说最终优化的结果最少包含一个单元(本例中)

必须定义一个拔模方向,如果不定义,那么就算最终优化出来结果,如果拔不了模,其结果也是无效的
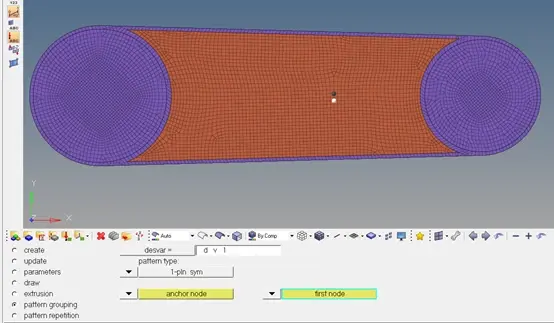
使用两点定义一个对称平面,即最终的优化结果是关于定义的平面对称
这个平面经过第一个点,并且平面的法向量为两点定义的向量
到此,设计变量定义完毕
2. 定义响应
定义两个响应:(1)体积分数
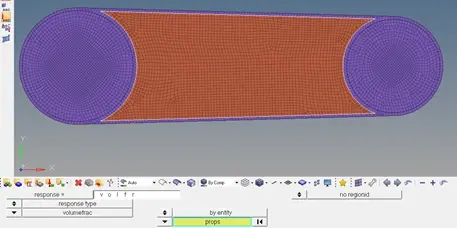
(2)挠度(也可以称之为柔度,与刚度对应)
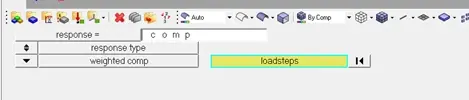
这里我选择的是权重挠度,什么意思呢?也就是说,我上面创建了两个工况L1和L2,在机器人实际工作中,旋转工况比上下运动的工况更频繁,那么就可以对这两个工况进行一个权重的设置,比如说L1的权重是2,L1的权重是1,那么后续优化分析中,算法会依据权重改变优化结果
3. 定义约束

将上面定义的响应中的体积分数,设置一个上限为0.2的约束,即橙色部分最终优化后,体积减少80%以上
4. 定义目标函数

将上面定义的响应中的挠度最小化,也就是柔度最小化,即刚度最大化
到此,定义完毕,提交计算,经过33次迭代,计算完毕
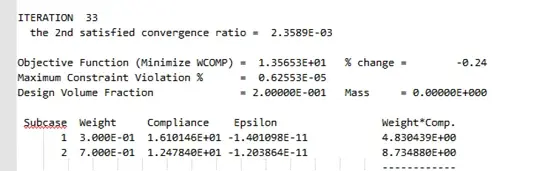

提示FEASIBLE DESIGN (ALL CONSTRAINTS SATISFIED),说明优化是成功的
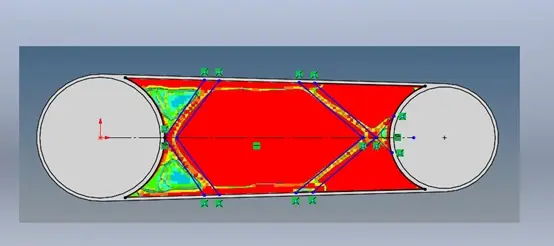
六、 后处理
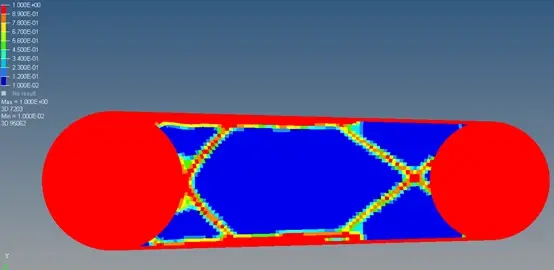
隔离出单元密度正常的单元
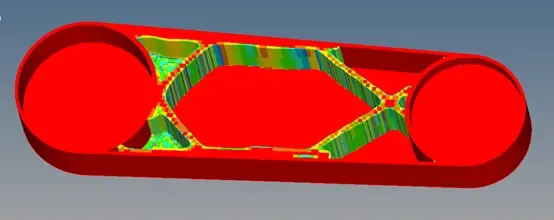
最终优化结果如上图所示