导数恒成立问题，今天学TA！小姚老师

导数恒成立问题

解题方式：

1.参变全分离：

步骤：

1.将参数和位置变量x分居不等式两侧

求含未知变量x的函数的最值

2.构造函数f（x），求导研究单调性，进而求出最大值或最小值

最后可得，a≥1

2.参变半分离：

部分题目全分离难以解决，此时应半分离，a与x不完全分离开，分离为f（a）≤g（a，x）

注：a也可位于左侧分离后应保证作图方便

分离后，画出图像，当图像与另一相切时成立

求切线斜率：

设出切点坐标（m，f（m）），对原函数求导，求出原函数在该点导函数的值即为切线斜率

用点斜式写出切线方程：

y－f（m）＝f＇（m）（x－m）

代入已知点（分离后含参数a函数的定点），求解方程即可得出f＇（m）

常见切线不等式：

例题：

1. 2022天津模拟卷（不需变形直接分离）

存在绝对值，全分离不易，固半分离

画出f（x）的函数图像：

画出g（x）＝｜x－a｜的图像

分析a对g（x）的影响

综合分析g（x）与f（x），寻找临界情况（切线、端点）

2. 2022南昌三模（需要变形进行分离）

遇到指数相对数，两边同时取对数

分离后得：xlnx≥alna

则构造函数：h（t）：tlnt

得h（x）≥h（a）

研究h（t）单调性，做出函数图像

（h（t）＝tlnt为常见的超越函数）

分析后可得a应在h（t）最小值，固a为定值1/e

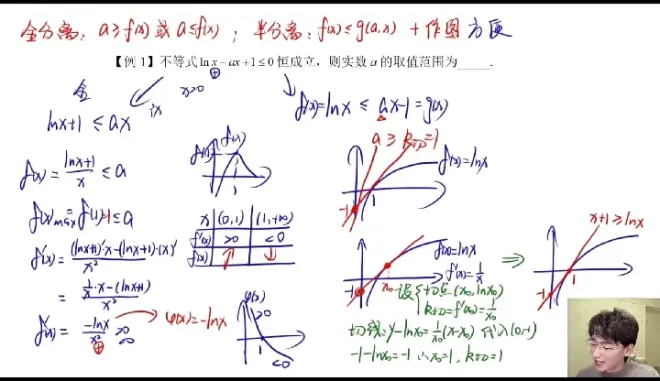
3.大题（大题一般用全分离）

全分离后构造函数h（x）求h（x）最大值

对h（x）求导，变形后分析分子与分母

分母大于零，此时只需要判断分子与零

构造函数，g（x）＝x－xlnx－1，研究g（x），得到g（x）≤0

则h＇（x）≤0，h（x）单调递减

则h（x）max＝h（1）＝1

固a≥1