高中物理 匀变速直线运动的研究—匀变速直线运动位移与时间的关系

这一节的内容讲一下匀变速直线运动如何求位移。根据前面学习的内容，方法一共有三种。

第一种，如果知道平均速度，那么位移就等于平均速度与时间的乘积，即，这是求位移最快捷的方法，能用就优先使用；

第二种，根据上一节讲的匀变速直线运动中，一段位移的平均速度等于该段位移初末速度和的一半。将上一种方法中的平均速度替换掉可以得到，也就是说知道匀变速直线晕的的初末速度以及时间，也可以求解位移；

以上两种方法，已知条件要么是平均速度，要么是初末速度，如果题目中没有这些已知条件，那就使用第三种方法。

第三种，将带入第二种方法的式子中，可得，即。在这个式子中，只需要知道物体运动的初速度，加速度和时间就可以求出位移。也就是说在初速度和加速度知道的前提下，物体运动的位移只与时间有关系。

注意：开始时（0时刻）物体位于坐标原点，所以在t时刻位移的大小等于该时刻物体的位置坐标，如果计时开始时物体位于坐标为的位置，那么在 t 时刻位移的大小就是，上面的公式就应该写为。

看一个例题：航空母舰的舰载机既要在航母上起飞，也要在航母上降落。

（1）某舰载机起飞时，采用弹射装置使飞机获得10 m/s的速度后，由机上发动机使飞机获得的加速度在航母跑道上匀加速前进，2.4 s后离舰升空。飞机匀加速滑行的距离是多少？

（2）飞机在航母上降落时，需用阻拦索使飞机迅速停下来。若某次飞机着舰时的速度为80 m/s，飞机钩住阻拦索后经过2.5 s 停下来。将这段运动视为匀减速直线运动，此过程中飞机加速度的大小及滑行的距离各是多少？

分析：舰载机在航母上降落的时候末速度为零，这是本题的隐藏条件，题目已经将两个过程规定为匀变速直线运动，所以根据已知条件中的初末速度，加速度和时间，利用公式就可以求解位移，但是在处理匀减速直线运动的时候一定要规定正方向，将矢量计算转化为标量计算。

解：（1）已知舰载机起飞做匀加速直线运动，初速度，加速度，时间 t=2.4s。求末速度。

由公式得。

2）已知舰载机降落做匀减速直线运动，以初速度方向为正方向。初速度，末速度，t=2.5s，求加速度 a 和位移 x 。

由公式得，加速度为负值，说明与初速度方向相反；

再由公式得。

飞机起飞时滑行距离为96 m。着舰过程中加速度的大小为，滑行距离为100 m。

注意：本题在解决最后降落位移的计算过程中，可以将计算加速度的式子变形后的带入中得，这样可以有效减少计算量，这是物理有别与其它学科的特点，一定要掌握。

这个公式也可以用v-t图像来理解，初速度不为零的匀变速直线运动的图像与坐标轴围成的面积是一个梯形，这个梯形的面积就是物体的位移，将这个面积分成两部分，下方矩形的长是时间t，高是初速度，矩形面积就是；上方三角形的的长是时间t，高是速度的变化量 at，三角形的面积就是；所以位移；如果初速度为0，就可以简化为。

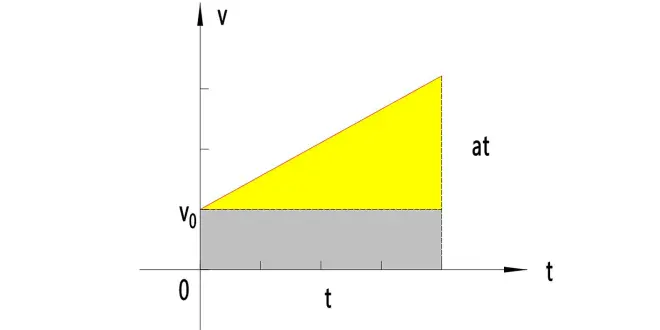
式子中的是由于物体具有初速度而引起的位移，是由于物体具有加速度而引起的位移。

注意：这个公式中的位移 x，加速度 a，初速度都是矢量，一般规定初速度的方向为正方向，加速运动a＞0，减速运动a＜0。如果减速运动的时间很长，有可能导致最后位移x＜0，这就表示物体最终的位移与初速度反向。

看一个例题：一个物体做匀变速直线运动，初速度，加速度大小为，方向与初速度方向相反，经过5s和10s的时间物体距离出发点的距离是多少？

分析：根据题目的已知条件可以判断出物体做匀减速直线运动，要规定正方向，再利用公式计算。

解：由于物体做匀减速直线运动，以初速度方向为正方向，已知初速度，加速度，时间，求位移。

由公式得，当 t=5s时，x=25m；当 t=10s时，x=0。

5s时的位移是25m，10s时的位移是0m。

这就说明物体做了折返运动，从A点出发匀减速运动先到达B点，此时速度减到零，再反向加速运动，10s时回到出发点A，在返回A点之前只是速度反向，而位移并未反向，位移是出发点到运动某一点的有向线段，以初速度方向为正，A点右侧所有位置的位移都是正值，直到到达A点并继续运动，位移才开始反向。

总结

求匀变速直线运动位移的三种方法