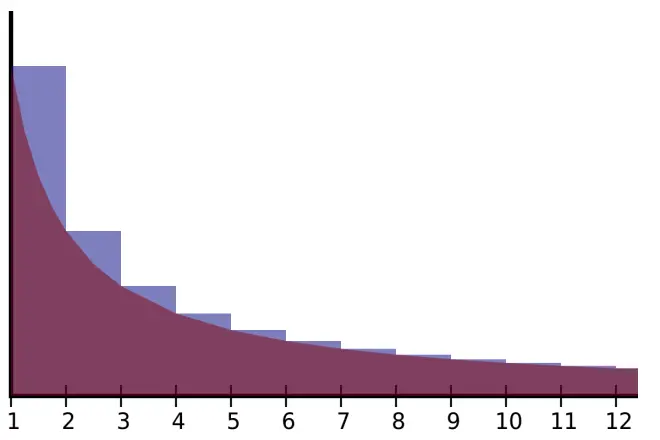
【趣味数学题】 欧拉-马歇罗尼常数
郑涛(Tao Steven Zheng)著
【问题】
题一: 求伽马函数(gamma function)的导函数。
题二: 欧拉-马歇罗尼常数(Euler-Mascheroni constant)定义为
用题一的结果来证明 。

【题解】
题一
考虑用极限改写伽马函数
使用莱布尼兹公式(Leibniz rule):
记得这个问题要把  改换为
改换为  !!!
!!!
由于
所以
题二
因为 ,
把 写成
;然后,令
和
,可得
因为 欧拉-马歇罗尼常数(Euler-Mascheroni constant)定义为 , 我们发现
欧拉-马歇罗尼常数的数值是大约 0.577216。