二阶常系数线性微分方程解
前言
由于经常计算电路响应,其电路模型经常出现二阶常系数线性微分方程(下文简称“二阶微分方程”或“微分方程”)。为减少重复工作,此处给出微分方程解析解,有实际问题时按需代入具体数值取结果即可。
微分方程解
1-微分方程
对于二阶弹簧阻尼振荡系统,或者LRC振荡电路,可列出其微分方程:
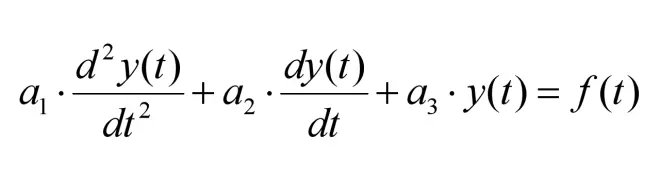
为了便于后文计算,此处定义一些符号:

由此,对二阶微分方程简化,并求出其拉普拉斯变换。其中y(0)为初始值,y'(0)为导数初始值:
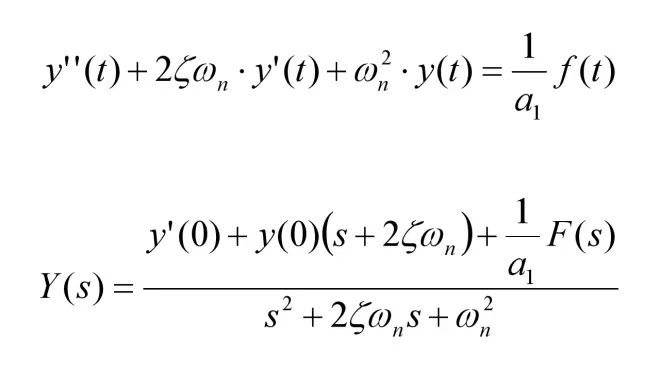
2-零输入响应
计算零输入响应时,令f(t)=0:
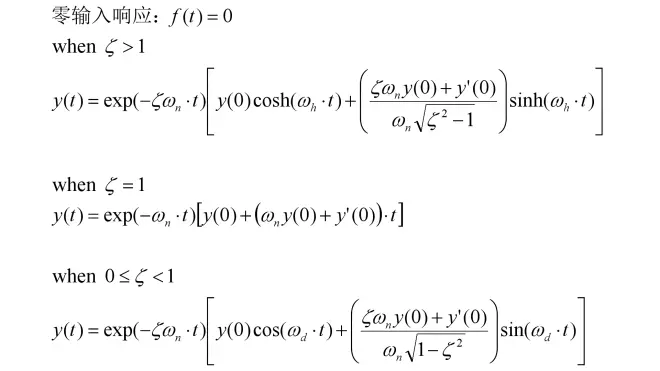
3-零状态响应——冲激响应
令y(0)=0和y'(0)=0,输入f(t)为单位冲激信号时:
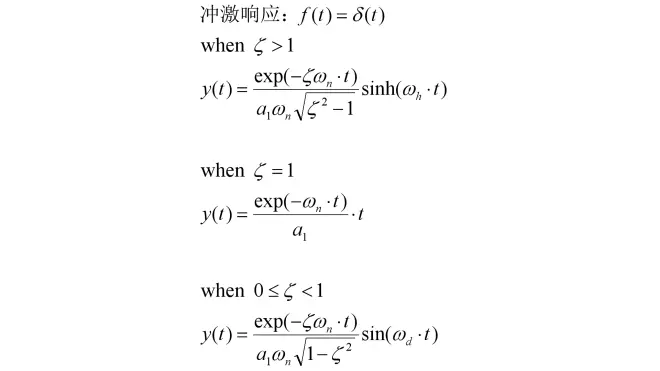
4-零状态响应——阶跃响应
令y(0)=0和y'(0)=0,输入f(t)为单位阶跃信号时:
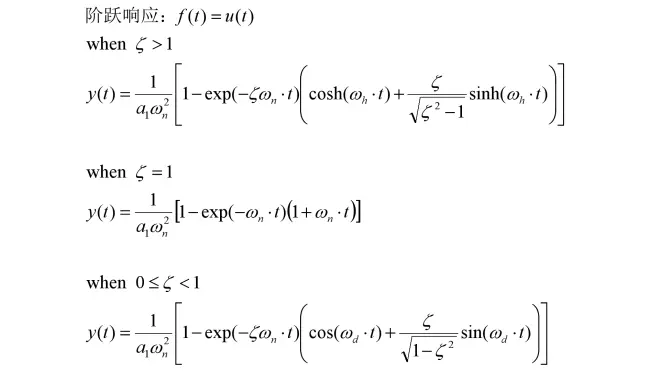

注:式子的简化是“有损”操作(arctan),即丢失了一些信息。所以简化式只在满足一定条件下使用,故保留简化前原式子。
5-阶跃响应关键参数
阶跃响应中有几个关键参数,其中有:
1、上升时间tr,曲线从稳态值的10%到90%所需的时间;
2、峰值时间tm,曲线超过稳态值并达到第一个峰值的时间;
3、调节时间ts,曲线进入稳态值±2%区间的时间;
4、超调量Ov,曲线最大峰值与稳态值之比(%)。
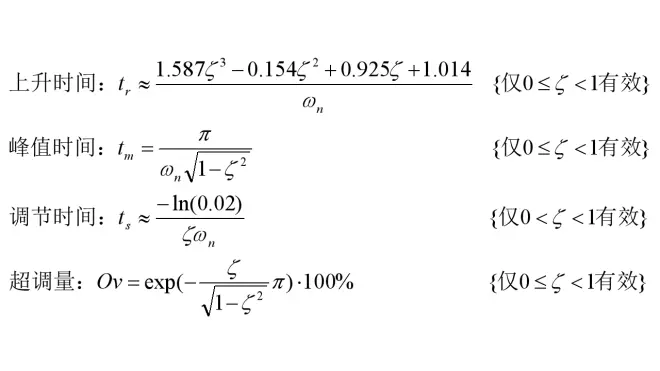
注:使用约等于号「≈」的式子是计算机迭代求解+回归分析得出的,非精确解。
6-零状态响应——正弦响应
令y(0)=0和y'(0)=0,输入f(t)为单位正弦信号时:
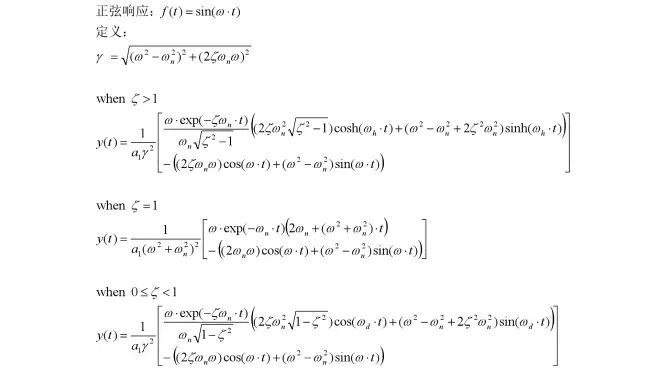

7-零状态响应——余弦响应
令y(0)=0和y'(0)=0,输入f(t)为单位余弦信号时:


8-正/余弦阻尼振荡响应关键参数
阻尼振荡响应有几个关键参数,其中有:
1、稳态振幅Amp;
2、稳态相角Angle;
3、共振振幅Amp_r;
4、共振频率ωr。
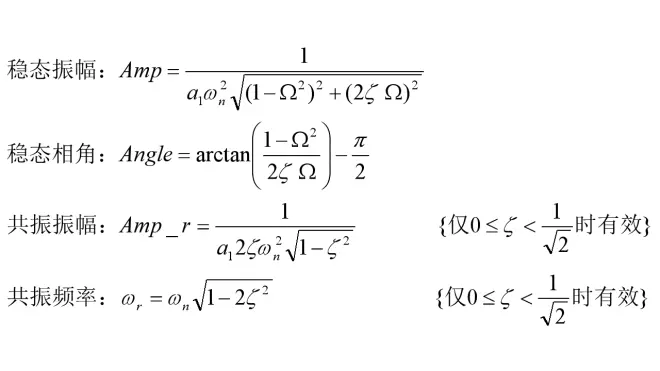
9-全响应
全响应为「零输入响应」+「零状态响应」。零输入响应为系统在原有的初始能量下自然响应,也叫齐次响应;零状态响应为系统在零初始能量下,由外加的输入引起的响应,也叫强迫响应。当系统为线性系统时,全响应则为两者效果的叠加。随着时间t推移,自然响应会逐渐趋于0,只剩下强迫响应(中的稳定参数)。
微分方程的导数解
1-微分方程
对于二阶弹簧阻尼振荡系统,或LRC振荡电路,前文算出的微分方程解一般代表「位移」或者「电荷」(位移隐含了力,电荷隐含了电压,差了个系数)。对其解求一阶导数后,解的物理意义发生变化,一般代表「速度」或者「电流」。现在求解:
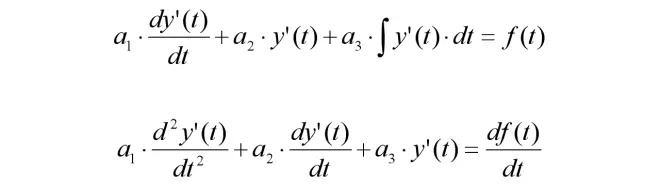
同样为了方便计算,定义以下符号:

由此简化二阶微分方程,并求出其拉普拉斯变换:
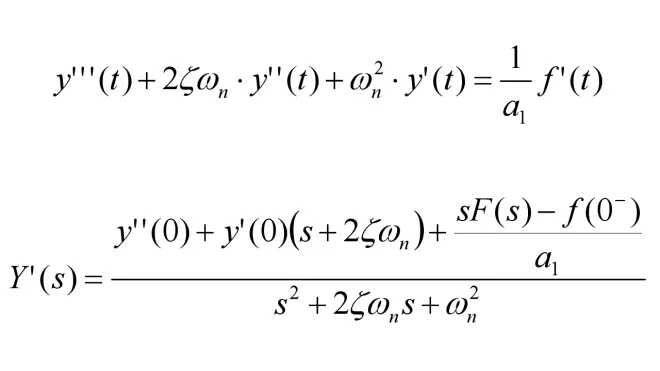
式子和之前的几乎一样,不过出现了新的初始值「y''(0)」。实际上,y''(0)的值是和y(0)有关联的。通过以下计算就可得到,并重新整理拉普拉斯变换式:
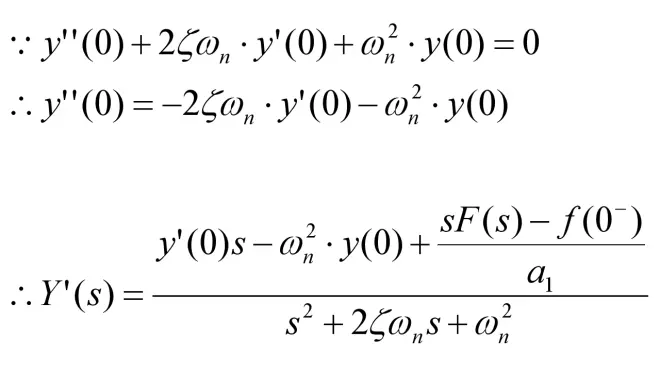
2-零输入响应
根据新的拉普拉斯变换式得出的式子,和之前的式子直接求导得出的是一样的:
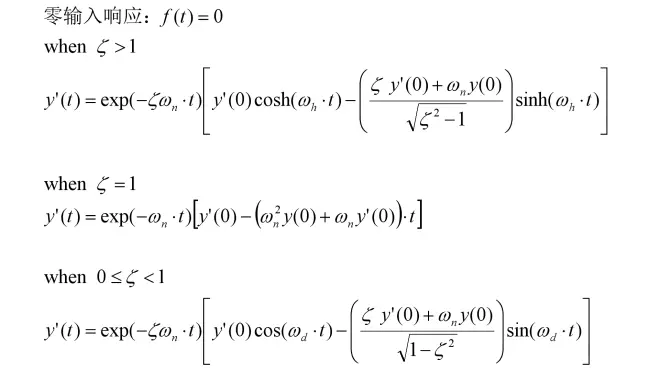
3-零状态响应——冲激响应
冲激响应可以认为“瞬间给予速度”,其式子几乎与y'(0)=1的零输入响应一样:

4-零状态响应——阶跃响应
由于阶跃信号的导数为冲激信号,所以“速度”的阶跃响应跟“位移”的冲激响应式子完全一致:
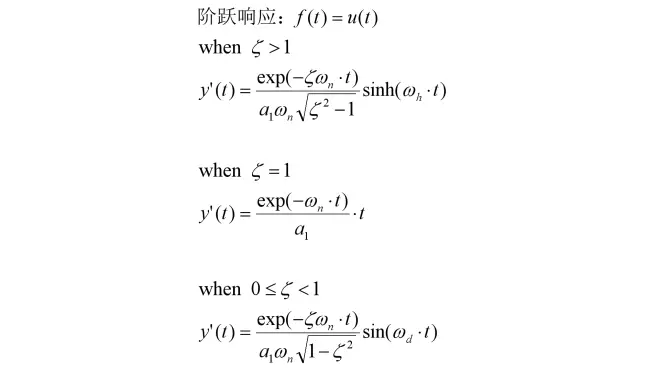
5-零输入响应——正弦响应
由于正弦求导即为余弦,所以“速度”的正弦响应与“位移”的余弦响应相似。注意由于求导会产生频率ω,两者式子还是有区别:


6-零输入响应——余弦响应
余弦响应求解跟前面三者不同,因为t=0时cos(0)=1,而前三者是=0。注意系统一般是因果系统,所以式子都是在t≥0时才有效,而在t<0时一律等于0。所以余弦在t=0的位置是个间断点,是突然加载到系统的,其【完整】的表达式为f(t)=cos(ωt)*u(t),对f(t)求导后,除了cos(ωt)求导产生的-ωsin(ωt)项外,还会带上一个冲激函数δ(t),即余弦响应为正弦响应的-ω倍再加上一个冲激响应:


7-正/余弦阻尼振荡响应关键参数
阻尼振荡的“速度”响应与“位移”响应有一点不同,同样计算这几个关键参数:
1、稳态振幅Amp;
2、稳态相角Angle;
3、共振振幅Amp_r;
4、共振频率ωr。
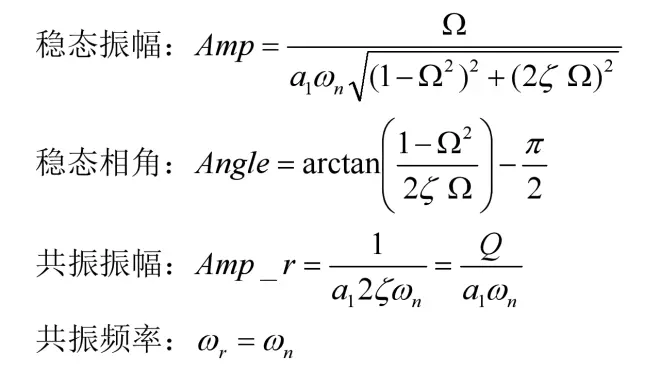
可以发现,“速度”共振频率与“位移”共振频率不一样。“速度”共振的最大值总在固有频率ωn上,而“位移”共振频率比ωn偏低,并且ζ小于0.707后才会出现。
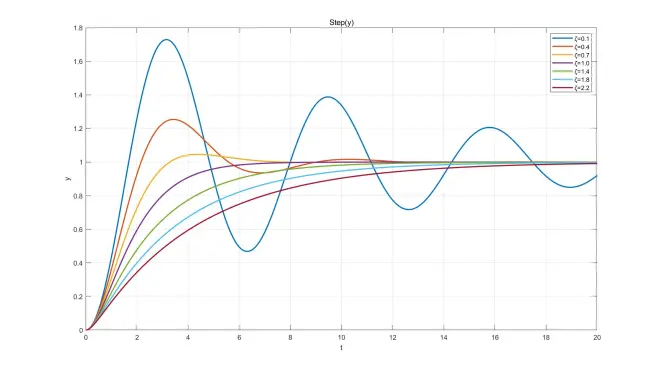
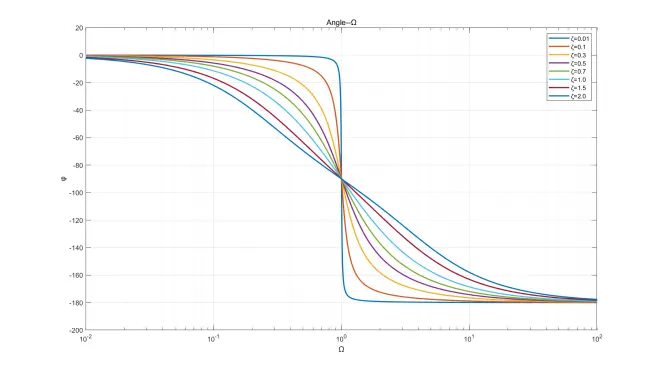
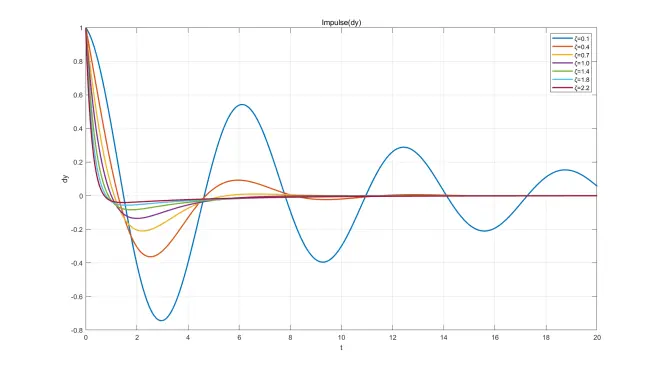
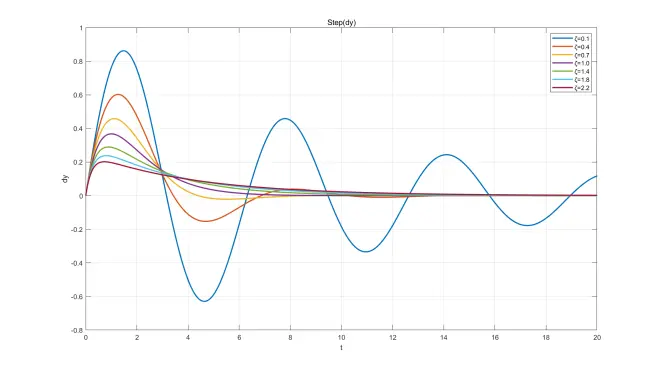
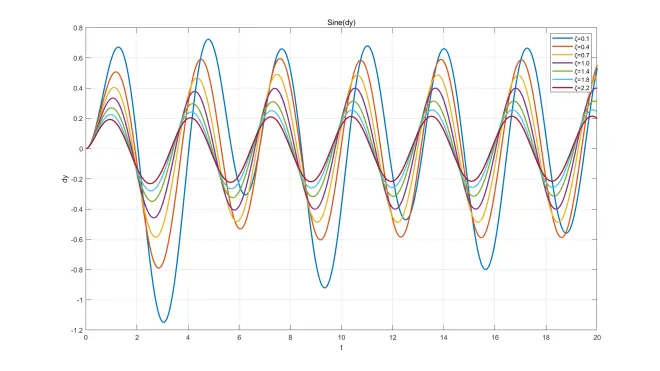
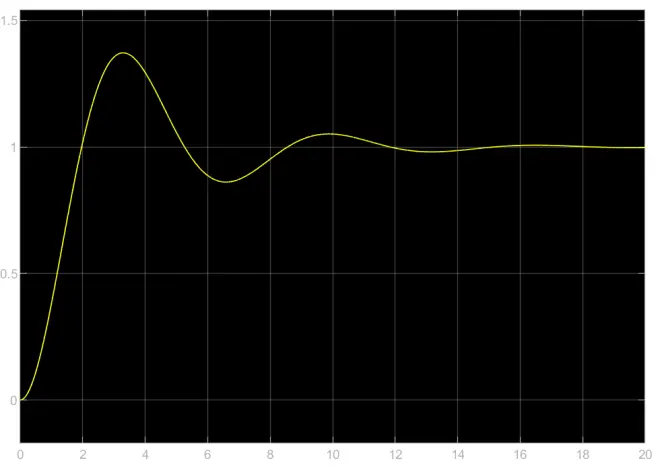
微分方程解函数图像
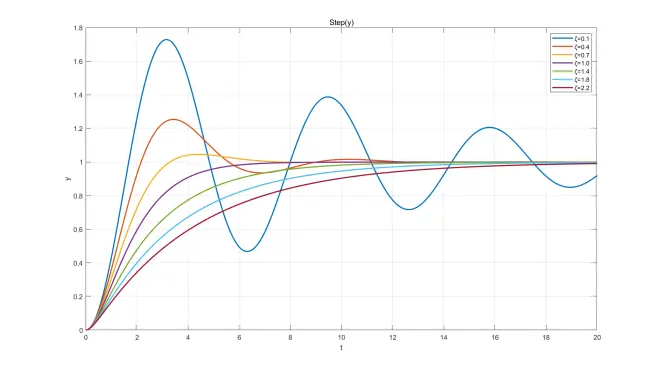
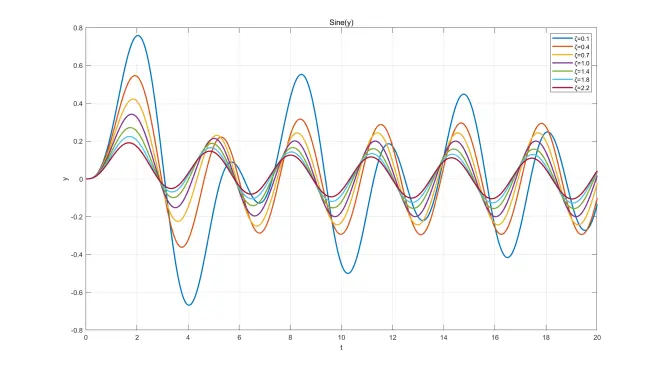
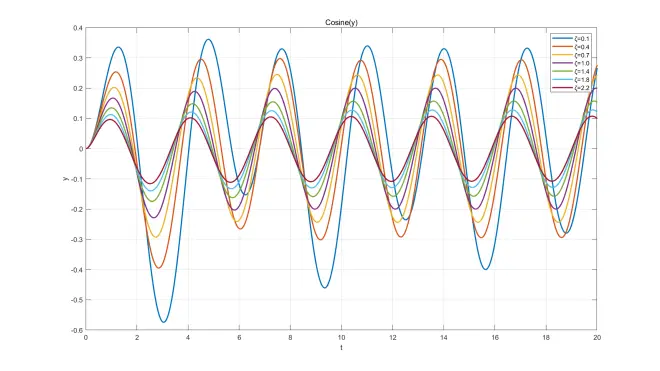
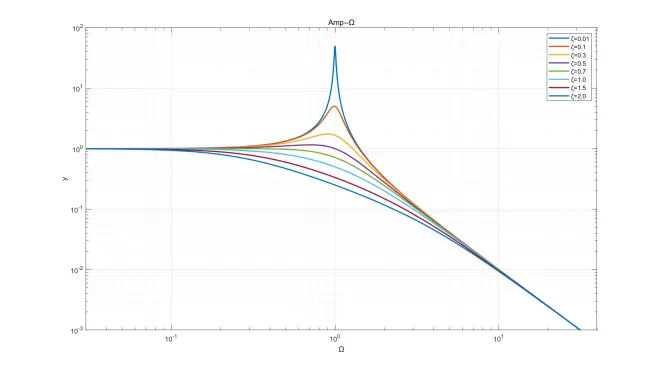
此处给出部分微分方程解函数,ωn=1、ω=2,ζ取不同值画在同一坐标系中,已标注图例。画图软件:MATLAB。
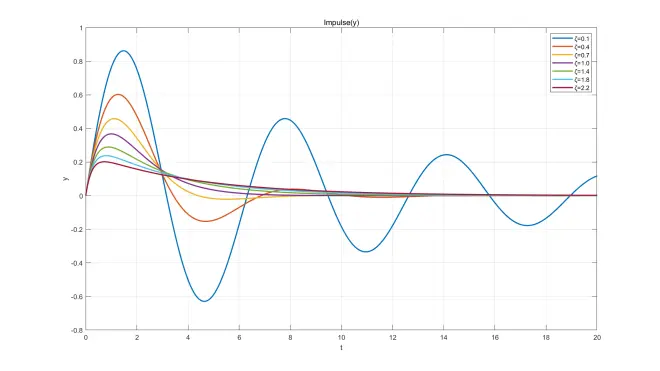
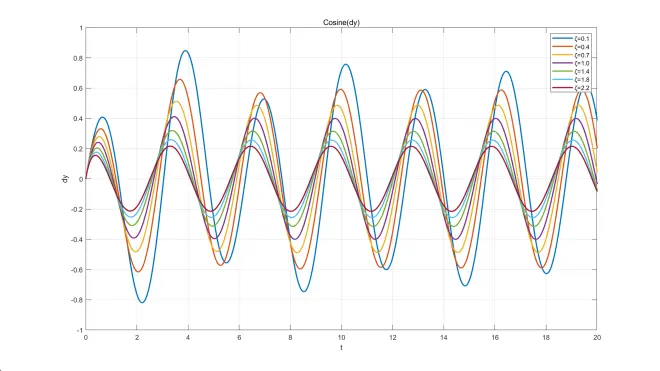
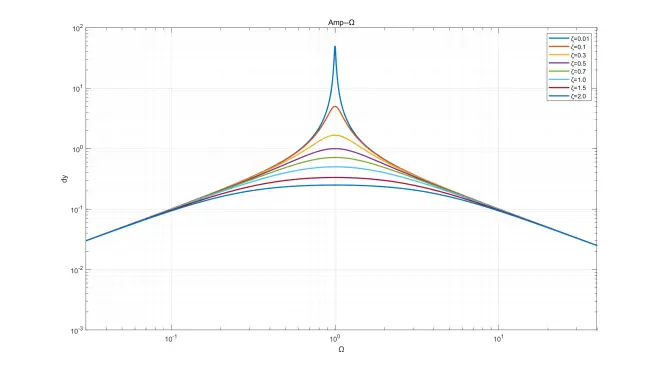
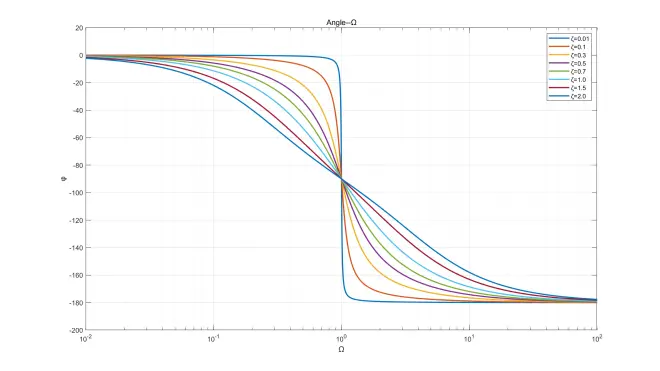
微分方程Simulink模型
此内容适用于计算机仿真,非手算。
由于计算机适合做积分,所以把微分方程式子调整下(注:a1已隐含在f(t)中),即可得:
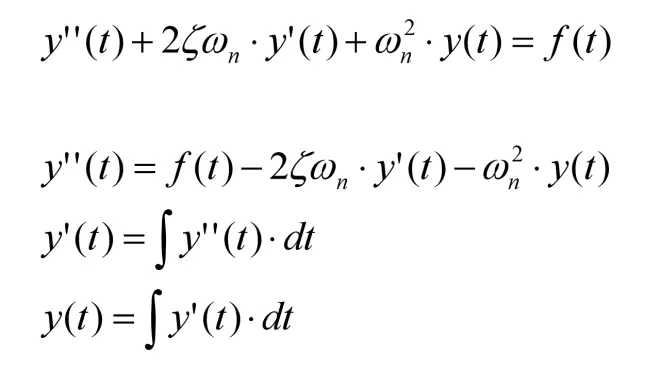
根据公式即可搭出仿真模型:
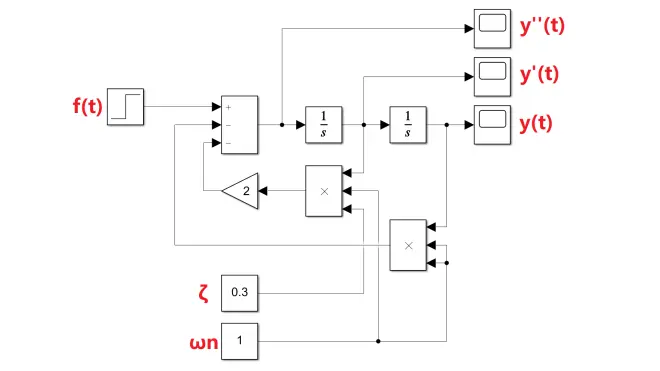
后记
文中的公式大部分手算推出,总计耗费25张A4草稿纸以及2个星期的时间,并使用计算机软件「GeoGebra」、「MATLAB」、「Excel」进行正确性检验(以及一些方程的回归分析)。本人尽力保证公式正确,但难免百密一疏,若读者发现错误,欢迎指出错误之处。(完)
by HD-nuke8800
2022/4/7
附录
以下为MATLAB绘制函数图像代码:
1、微分方程解「
」
2、微分方程导数解「
」
3、绘制函数图「
」

