“Trivial”的四度空间
“Faux Amis"节目不光讲词汇、语源,有时也要给大家科普一下数学知识。(^v^)
就从“trivial”的四维空间说起吧。

上一期 “Faux Amis" 节目提到了法语“trivial”的“粗俗,猥亵”义。而“trivial”一词在数学里还有个特殊的含义: "平凡的"。(英语和法语都是一样的)。
因为 trivial 一词有“琐碎的,微不足道”(négligeable, peu important)的含义,所以在数学里用 trivial (平凡)来描述“最简单的”,或“不言自明”的解。在代数里,就是所有变元都等于零的那个解。当然,与 trivial solution(平凡解)相对应,还有non-trivial solution(非平凡解)。

很高深吧?不要紧,举个拓扑学”的例子你就懂了。(^v^)
大家都会系鞋带吧?也都见过“中国结”吧?
下面这张图里就是一个“结”:

纽结理论 Knot theory (La théorie des nœuds) 是数学里拓扑学的一个分支。专门研究“结”的。
在拓扑学里,结分为“平凡结”(trivial knot )和“非平凡节”(Non trivial knot)。
下面这张图里就是一个“平凡结 (nœud trivial) ”:

Trivial knot(平凡结)指的是 “最简单的结”, 就是圆环。上面的绳圈轻轻一拉, 就变成圆圈了吧?

凡是能变成圆环的结就是平凡结(trivial knot)。左边的结拉伸后, 就变成右边的圈了。
变不成圆环的,就是非平凡结(Non trivial knot (nœud non-trivial))
三叶形(trefoil)是最简单的“非平凡结”。

下面这个结又是怎么回事呢? 分明是个 non-trivial knot(非平凡结) 呀, 怎么却玩起了"穿越", 变成了平凡结(trivial knot)了呢?
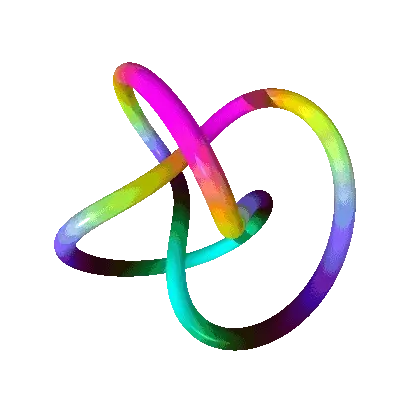
原来, 动画里显示的是个四度空间里的结. (终于说到“四度空间”啦!^v^)
根据数学家的研究,在四度空间里,是没有 non-trivial knot(非平凡结)的,而 只有平凡结(trivial knot). “打结”,“系绳扣”这种事,只能发生在“三度空间”里。
如果不能打结, 你还能系鞋带吗?
所以,如果有一天,你发现鞋带系不上了,你一定是来到了“四度空间”!
扩展阅读:哈佛大学数学系的证明:No knots in 4D(为什么在四维空间无法打结)

哈佛大学数学系的证明:
https://abel.math.harvard.edu/archive/21a_spring_06/exhibits/unknotting/index.html
No knots in 4D为什么在四维空间无法打结(哈佛大学数学系的证明)
A knot is a closed curve in space. A knot is called trivial, if one can deform it to a simple unknotted circle without having any selfintersections at any time. It is quite easy to see that in four dimensions, there are no nontrivial knots. You would not be able to tie a shoe in four dimensional space.
We use color as the fourth coordinate. The fourth dimension is the "Hue value" between 0 and 1. It labels the colors similar to the rainbow. If we color the knot, we place the knot in four dimensional space. We have a parametrized curve r(t) = (x(t),y(t),z(t),c(t)). The three first positions (x,y,z) are the positions of the point on the curve and the four position c is the color at that point. If we unknot the knot, we can now do that in four dimensions as long as the colors are differents, where the projection of the curve to three dimensions intersects.
为什么在四度空间里没法系鞋带呢?在动画图里显示的,就是个四维空间的结,第四维是以颜色表示的。在三度空间里的“非平凡结”,在四度空间里会发生“穿越”:只要是颜色不同的线段,就可以互不相扰地彼此穿插。这样,再复杂,再“纠结”的 knot(非平凡结),也可以很容易地打开成圆环(平凡结 trivial knot)啦。
所以,在四度空间里没法系鞋带啦!
怎么样?数学家研究的问题,是不是很 trivial 呢?(^v^)

鞋带系不上,这已经由哈佛大学的数学家证明了。(详见前面的证明。B站这里有学数学的吗?^v^)
同样, 在"四度空间" 里也吃不了面条啦,这和系不上鞋带是同一个道理:面条会从筷子上“穿越”过去。用叉子也吃不了通心粉啦! 不过, 用不了筷子,可以用嘴“吸”面条吧?

更有甚者, 在"四度空间" 里,裤子会掉下来,这是因为皮带环扣也会玩“穿越”啦!(^v^)
其实,不光是裤子,一切靠带子,系绳,环扣连接的衣物,都会掉下来 ! 更有甚者,一切纺织品都会“解体”,变成一堆“乱线头”——因为,织物里的经线和纬线也会互相“穿越”啦。 (^v^)
很麻烦啦:穿不了纺织品,可以穿兽皮吧? (^v^)

好啦, 高深纠结的“四度空间”就先说这些吧。有点"trivial"啦。大家是否都明白了呢?
现在,要考考大家:
问题:如果哪一天,你的鞋带突然系不上了,你一定是 __________。
A:在做梦
B:在三岔路口。
C:黄段子讲太多了。
D:来到了“四度”空间。

参考答案:D.来到了“四度”空间。
现在,请你检验一下,你那里是否是“四度空间”呢?(^v^)

