陶分第十一天（3.6）

应该没记错日子吧。

本节讲的是基数，也就是自然数的另一个层面，用来计数集合中元素的数量。本节涉及的主要证明能力是:(1)结合已有的结论来证明，尤其是集合和函数的几节，也稍微涵盖了像，笛卡尔积，自然数的内容。(2)构造一个明确的双射函数。先声明这个函数，接着证明这个定义下函数的存在性，单射性，满射性。(3)数学归纳法，总是会用到命题3.6.14(a)(b)，和引理3.6.9。

（这次没对答案，如果对你解题产生了误导up当场滑跪(泪)）

相等的基数

 我们如果可以在两个集合之间构造一个双射，那么两集合的基数是相等的。这与我们掰手指头算数的原理一致。

 基数相等也是一种等价关系。因此满足四条公理。

3.6.1，证明相等的基数是一种等价关系。

 (1)构造函数f：X→X满足f(x):=x

(2)可逆函数的逆是双射的（习题3.3.6后半截）

 (3)双射是传递的。（习题3.3.7）

 3.6.5，照应了定义3.5.4。f(x，y):=(y，x)

 3.6.6，猜测为u：g→f（这里是元素到元素，输入法没有，用加粗表示），g：(b，c)→a，f：c→α，α：b→a。a，b，c分别属于A，B，C。u(g):=f⇔g，f满足g(b，c)=(f(c))(b)。没时间搞，可能是对的。

基数为n

 建立其集合与自然数集的关系。

3.6.2，在归纳法里面用的很多。

 利用习题3.3.3的结论。

3.6.9，抽屉原理还挺有用的，而且还可以扩展，得到更广义的情况。

 利用反证。

基数唯一

 除了命题本身之外，还有一个有意思的引理：X的基数为n且n大于等于1，则对x属于X，X-{x}的基数是n-1。

有限集

 在证明的时候都会要证到这个性质。但基本没有人会照着定义来的吧。。。

3.6.3，自然数集的有限子集是有界的。

3.6.7，利用命题3.6.14(c)(d)，再利用像的知识。

3.6.8，利用像和逆函数构造双射函数h⁻¹(b)，再以此定义b∈f(A)时g(b):=f(b)。

基数算数

 蛮有用的，习题细说。

3.6.4，活用归纳法。

 (a)可以不用归纳法，设#(X)=n，存在双射函数g。构建函数f：X∪{x}→{i∈N：1≤i≤n+1}，满足x∈X，g(x):=f(x)，x∈{x}，g(x):=n+1。接着三板斧证明就可以了。注意，当我们指出集合的基数时，就已经证明了它是有限集。

 (b)记#(X)=n，#(Y)=m。对n归纳，0的情况易证(利用习题3.6.2的结论)。接着假设n的情况结论成立。此方便起见我们假设#(X∪Y)=k≤n+m

 注意我们是对任意基数是n的集合成立结论的（尽管n本身是确定的，但X是无限定的集合。）证明对集合A，有#(A)=n++成立结论。这里可以利用到引理3.6.9，结合单个选取（引理3.1.6），取出a∈A，则有#(A-{a})=n。进而#((A-{a})∪Y)=k≤n+m，进而#(((A-{a})∪Y)∪{a})=k or k+1≤(n++)+m（用到了(a)和序不变(命题2.2.12(d))）

 ((A-{a})∪Y)∪{a}=A∪Y，{a}⊆Y⇔{a}∪Y(习题3.1.5)，此时#(A∪Y)=k，否则为k+1。

 若此时A∩Y=φ，显然(A-{a})∩Y=φ，所以此时k=n+m，且由上{a}不包含于Y，故#(A∪Y)=k+1=(n++)+m。

(c)类似的配方，第二个内容从n=1开始证，顺便证个引理：X为单元素集当且仅当#(X)=1。

(d)仍然归纳法。当#(X)=0时，f(X)=φ，有0≤0，并且由习题3.3.3的结论，此时f一定为单射，也满足0=0

 类似的配方。定义f：A-{a}→Y，满足f(x):=g(x)。再设y∈Y，y=g(a)。

 最后#(g(A))=#((g({a}))∪g(A-{a}))≤#({y})+#(f(A-{a}))=n++。

(e)类似的配方，略。

(f)呜呜呜手打要拖更了。。。

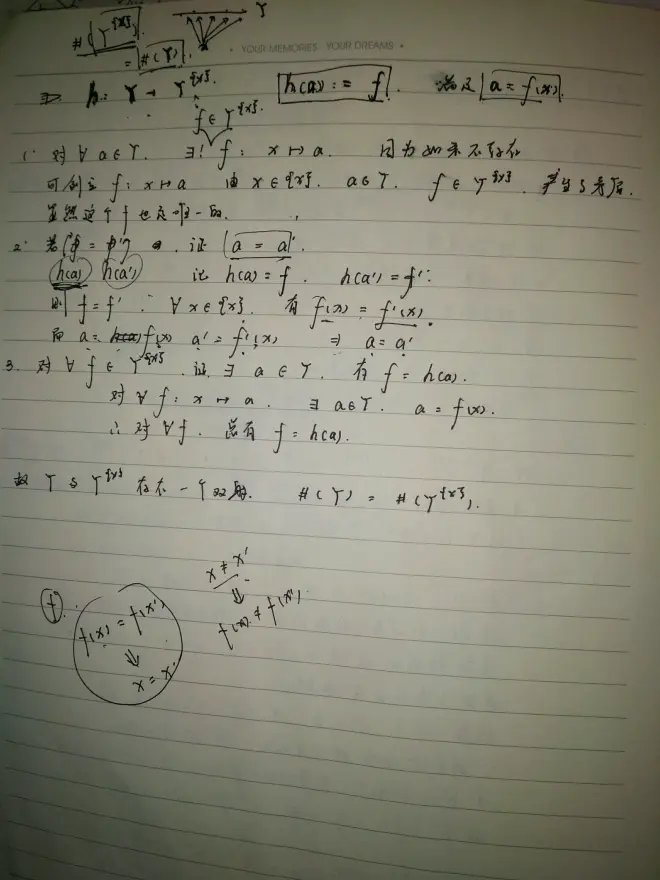
3.6.9，配合3.6.14食用更佳。

 em，匆忙写的证明，利用了习题3.1.10。

 A=(A\B)∪(A∩B)，B=(B\A)∪(A∩B)，A∪B=(A\B)∪(A∩B)∪(B\A)，由于三者不相交。根据3.6.14(b)，有#(A)+#(B)=#(A\B)+2#(A∩B)+#(B\A)=#(A∪B)+#(A∩B)

就这样。