[Algebra] Omar Khayyam's Cubic
By: Tao Steven Zheng (郑涛)
【Problem】
Omar Khayyam (1048 – 1131 AD) solved cubic equations of the form by transforming the problem into finding the intersection of a circle and a parabola:
where are positive numbers.
Part 1: Determine in terms of
.
Part 2: Use Omar Khayyam’s method to solve the cubic equation by sketching the two conic sections and locating the intersection points.


【Solution】
Solution for Part 1
Write the first equation as and the second equation as
. Substitute the second equation into the first equation to eliminate
, and obtain
.
Consequently,
or
Matching terms with the cubic equation gives
Since are positive numbers,
Solution for Part 2
For the equation ,
and
. Thus,
and we need to graph
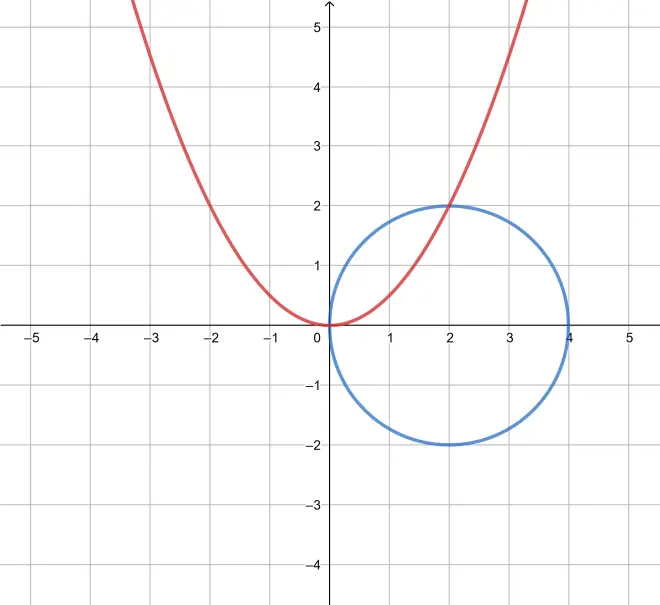
Intersection points: (0,0); (2,2). When the values of is substituted into
, we find only one solution to this cubic
.