S405 概率实验难演示?(上)
在人教版五年级数学的学习中,学生第一次接触到“概率”,到初中九年级时,对机率有进一步认识,接触到实验机率模拟的概念。但是课堂上老师可以通过让学生“掷一掷”初步建立可能性的概念,随着学习的推进,如何看到“可能性”的分布趋势,需要大量的投掷才能够实现。这时候,计算机模拟就可以帮得上大忙了,趋势也很容易观察到。本次课程分为初阶和进阶两部分,能够帮助我们快速模拟概率实验,今天课程的效果图如下:
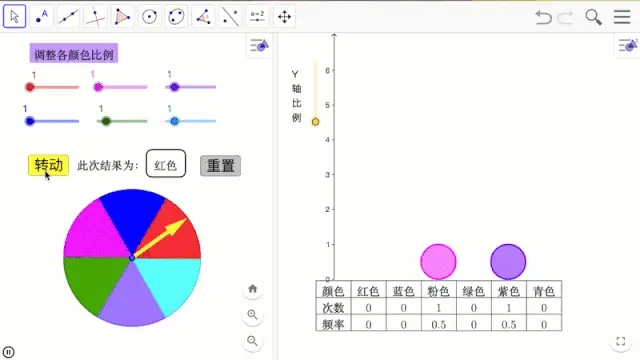
首先进行问题拆解,效果图分为两部分:一部分是左边的实验模拟【今天的课程内容】,一个是右边的结果统计。
我们可以先做一个均分的圆盘,让指针在上面转动;然后让指针可以随机转动并展示结果;最后修改参数,使之变为可调节比例的圆盘。
本节课的关键理解为:
对随机模拟实验要掌握哪些变量设为随机变量,并采用哪些观点来解释随机的结果。
你将学会:
1. 使用指令画扇形;
2. 使用指令修改图形颜色;
3. 设置随机变量;
4. 定义一个序列并取用集序列内的元素。
1 建立圆盘和指针
A. 如何画一个六等分的圆呢?
方法一:首先,我们最直接想到的就是使用Circle指令,画一个圆,然后把每个扇形用三个点连接起来。
扇形指令:CircularSector( <Midpoint>, <Point>, <Point> )【翻译:圆扇形(圆心,点1,点2)】
这里的点因为在圆上,我们用极坐标可能会是一个比较好的方式进行绘制。
极坐标:(半径;弧度)
【与点坐标,你发现极坐标的表示有什么不同了吗?答案见文末①】
你可以使用指令来进行绘制吗?【答案见文末②】
方法二:利用【序列】指令找到扇形的分割点,连接圆心与分割点。
分割点:
O=(0,0)
Ps=Sequence((1;k/6*2pi),k,1,6)
绘制扇形:
Cs1 = CircularSector( O, Ps(6), Ps(1) )
以此类推绘制其他5个扇形。
B. 设置扇形的颜色
设置颜色指令:SetColor( <Object>, "<Color>" )【翻译:设置颜色(对象,"颜色)注意:需要以#开头")】
【如何找到你想要的颜色编号?答案见文末③】
需要建立【按钮】来实现改变颜色的操作。
【按钮】-【设置】-【脚本】-【输入指令SetColor】【答案见文末④】
C. 绘制指针
我们可以把指针看做是一个向量,绘制一个起点确定,终点可调节的向量即可。
向量:Vector(Point)【翻译:向量(点(默认起点为(0,0))】
此点我们依旧可以用极坐标来表示。
spinner = 360【设置滑动条】
tip=Vector(1;(spinner/360)*2Pi)
效果如下:
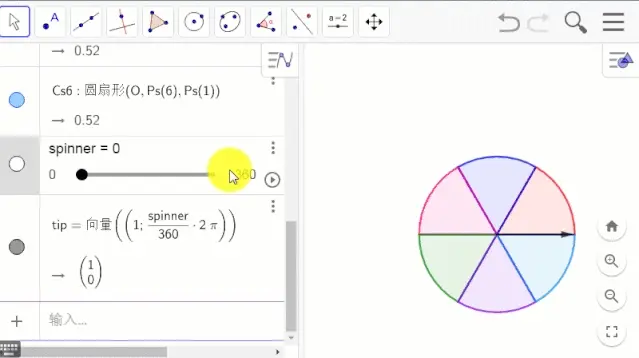
2 让指针随机转动并显示答案
A. 让指针随机转动
第一步中产生的指针可以进行转动了,但不是随机的,所以我们要把指针的终点设置为一个随机数即可。
区间随机数:RandomBetween( <Minimum Integer>, <Maximum Integer> )【翻译:区间随机数(最小数,最大数)】
方法一:讲指针的滑动条设置为一个随机数即可。步骤:
新建按钮
脚本
spinner=RandomBetween(1,360)
启动动画()
这样,我们就把tip 的一个参数通过随机数实现了。效果如下:

我们发现指针是直接跳到终点的,那我们可以让他转动吗?那我们规定它转动的圈数和角度可以实现吗?也就是spinner需要由去圈数和转动的角度两个参数决定,即spinner=turn*360+end【turn-转动的圈数,end-最后一圈转动的角度】
方法二:设置转动的圈数和角度
新建参数turn 和 end(范围可以自己定)
设spinner的最大值为turn*360+end【操作:
spinner-设置:
最大值为turn*360+end】
设置指针只转一圈【设置-递增(一次)】
效果如下:
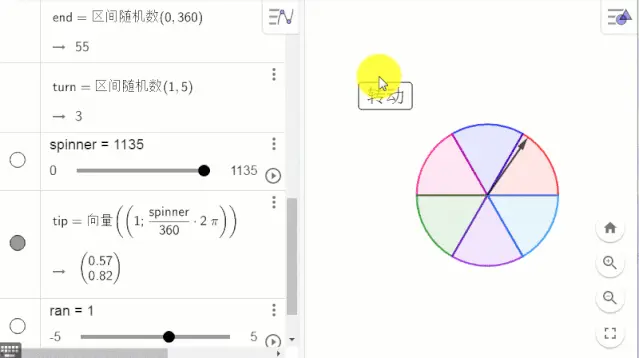
B.显示转动效果
上面的随机数中,影响颜色的因素是除去转动的整圈数,再看它转动的度数。我们可以给每个度数的范围(小于360的)都标记一个颜色的名称,计算出终点的所在第几个60度,然后与标记的颜色序列进行挂钩,即可知道是哪个颜色。
指令如下:
names = {"红色", "蓝色", "粉色", "绿色", "紫色", "青色"}【定义了一个序列,里面从第一个到第六个分别为6种对应的颜色】
endAngles = Sequence(60*k, k, 1,6)【最终的角度是里面有几个60】
resIndex = countif(x < end, endAngles) +1【上面的商+1即为取names里面第几个颜色】
resName = names(resIndex)【显示第k+1个颜色】
效果图如下:
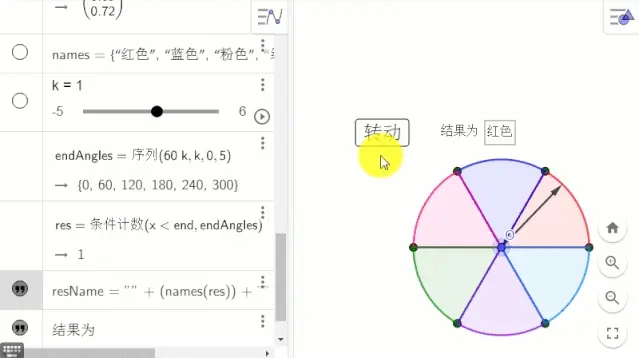
C. 颜色随指针的转动而动
因为我们最终的度数,所以直接就显示了最终的颜色,那我们可以把最终的度数换成正在改变的度数也就是“spinner”,因为spinner可能是大于1圈的,那么我们就去和360的余数作为求解颜色的角度,用到指令求余数:
求余数:Mod( <Dividend Number>, <Divisor Number> )【翻译:取余(被除数,除数)】
如何修改B中的指令呢?【答案见文末⑤】
效果图如下:

3 调整圆盘比例
A. 建立6个滑动条
六个分别用于调整每一块的比例。让 s1, s2 的范围是 1~6,s3~s6 的范围是 0~6。
B. 先将六个滑杆并为一个序列 ss,要计算各颜色比例,先求综合,再计算 ps 。
ss = {s1,s2,s3,s4,s5,s6}【把六个数放在了一个叫ss的数列中】
total = sum(ss)【求六个数的和】
ps = sequence(ss(k)/total, k,1,6)【分别计算每一部分所占的比例】
C. 找到每个扇形的两个点
接着要将扇形的端点作分割,等于要计算每个扇形的终点位置。【思考:如果直接用ps中的六个数会怎么样】【答案见文末⑥】
sps=Sequence((sum(ps,k),k,1,6))
D. 修正Ps
Ps=Sequence((1;k/6*2π),k,1,6)【中的k/6替换为:sps(k)】
endAngles = Sequence(60*k,k,1,6)【中的60*k替换为360*sps(k)】
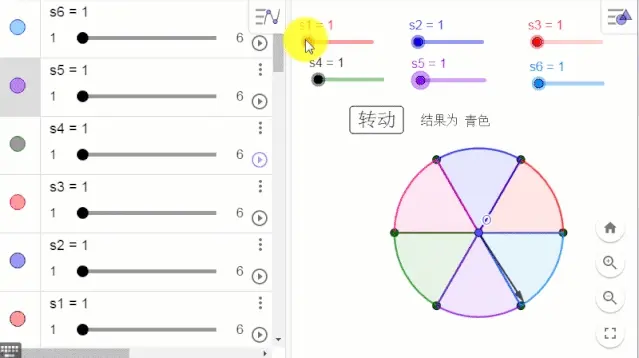
一个随机模拟的演示实验就做完了,老师还可以把它作为课上“随机”点名的工具,是不是特别刺激?你可以做哪些修改,让一些同学被点名的概率变大吗?
答案区
① 中间使用“;”进行连接,这样计算机才可以识别是极坐标哦~
② O=(0,0)
Cs=Sequence(CircularSector(O,(1;(k/6)*2Pi),(1;((k+1)/6)*2Pi)),k,0,5)
③ 选择任意一个对象-【设置】-【颜色】就可以看到对应颜色的编码了
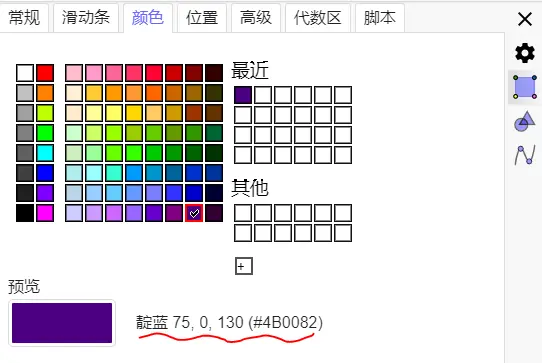
④ 方法一的图形设置颜色
你会发现没有办法设置颜色,GGB里面只能是一个序列一个颜色,所以这里无解了~你可以试一试还有什么方法吗?
方法二的图形设置颜色
SetColor(Cs1,"#FF0000")
SetColor(Cs2,"#0000FF")
SetColor(Cs3,"#FF0088")
SetColor(Cs4,"#008800")
SetColor(Cs5,"#8800FF")
SetColor(Cs6,"#0088FF")
⑤ 把end 替换为Mod(spinner,360)
⑥ 可以尝试一下,出现的效果是每个扇形的起点都一样,就没有办法组成一个圆。
小结
在这部分我们先实践,机率转盘模拟的前半段。制造一个随机事件(在圆盘转动的圈数与角度),并解读他的结果(判断停留点位在那个区域)。核心概念就在于产生随机性与解读随机性。
当然这只是单次的结果,不容易做些分析,在这后续的进阶视频我们将要来分析每次的结果,并用统治图表让他可以清楚地显示。
挑战
有些随机转盘是,指针一直朝上,但让着色的圆盘会转动。如果是要实践这样的结果,那你觉得课件该如何设计呢?
另外,关于随机性的课件,目前也有两篇相关的介绍,一个是利用随机出题来实现自动大量出题。另一个是硬币的正反面模拟统计。大家可以试着只看结果图,来思考如何拆解制作。思考后,自己动手卡住时再看视频解说。
平方数自动出题

丢铜板机率模拟:

相关资料
【GGB】https://www.geogebra.org/classic/nbq6vbaq
【Bili】https://www.bilibili.com/video/av75148091
人教版九上 25 章《体验用频率估计概率》

