【二项式定理】保姆级梳理，重点题型一网打尽！

本节内容👇

讲解框架👇

二项式定理怎么来的？（内涵）

规范书写（写出它的通项公式）即

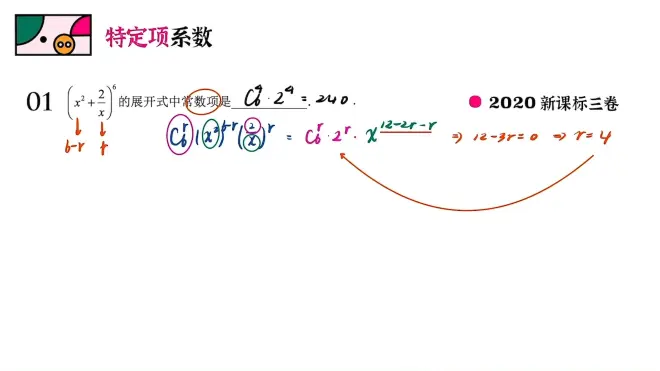
一。特定项系数

例题

要求常数项，即x⁰时，所以只需使12-3r=0求得r

上面所用通项法对这种较简单的题目来说就足够了，但当题目变难一点👇

此时再使用通项法就会很复杂，我们需要掌握其他方法

瞪眼法

发现只有此时，才是常数项👇

注意：写系数时，除了x之外的一些常数（如 2，也跟着x⁻¹出了4次）

所以常数项应为

小练一下（多因式相乘）

对于第一题，可以用分配律的方法👇

第二题，就必须从本质出发，先按题目要求进行分配👇

之后写法，这很重要（这样写不易出错！！）

总结：题目简单——通项

复杂——瞪眼法

（多项和展开）用瞪眼法同样可写

左右都复杂

例题

观察题目发现出现了很多次（x-1），考虑换元，即👇

最后得到👇

二。二项式系数

什么是二项式系数？

具体考点👇

知识点二的证明会用到一会儿要讲的赋值法

再进一步推理，得到👇

二项式系数最值是二项式系数知识点中最难的

三。系数最值

二项式系数和系数区别

那如何求系数最大值呢

一个一个求，再判断最值太费时间（右上角）

离散型函数又不能求导（左半边）（点怎么能求斜率呢）

可利用数列的方法

具体如👇

下面两项加起来等=8

最后得到

上下两个式子具有一定的关系

把r→r+1

把≥→≤

得到

所以我们解一个方程即可

最后最大值应为（在最上面👇）

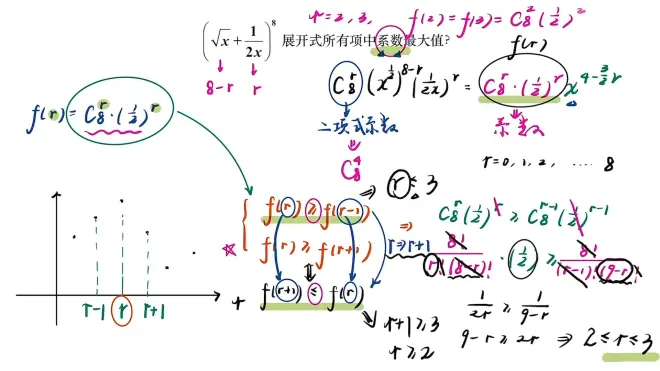
总结一下

四。赋值法

01 02 较为简单

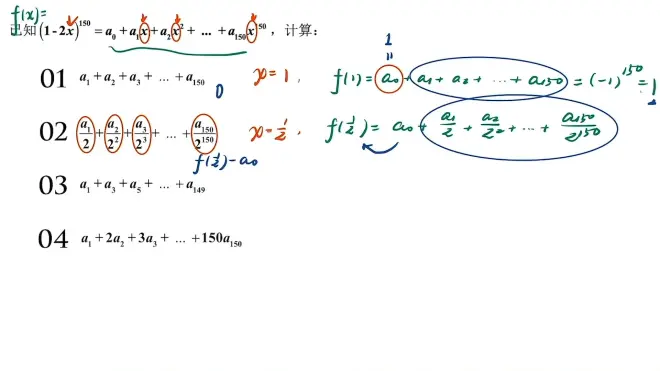
03 （求偶或奇，代x=-1,x=1，之后联立👇）

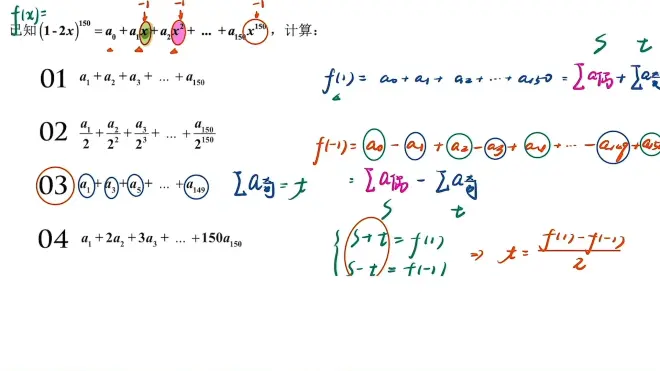
04 （用到求导）

完结*★,°*:.☆(￣▽￣)/$:*.°★* 。