孪生子佯谬在Rindler坐标下的计算

为了方便起见，考虑一个匀加速运动。设想的场景是这样的：孪生兄弟Alice和Bob一开始都在地球上（近似为惯性系）。后来Bob搭乘飞船上天，这艘飞船的运动方式是这样的：先有一个很大的初速度，然后一直沿着初速度的反方向点火，持续减速到停止然后重新加速回来。也就是一个匀加速直线运动。

假设Bob的加速度为a，最远离Alice的距离为d。

我们想问的是：从Alice的视角看，Bob的年龄是如何变化的？从Bob的视角看，Alice的年龄是如何变化的？

Alice视角

采用这样一个坐标：

直截了当的计算给出：（这个结果把两个时间“平移”到同一个起点）

所以，在相遇的时候，Alice和Bob的年龄分别为

那么很显然，Bob会年轻一点。

在Alice的视角下，整个过程中Bob年龄的变化为：

从头到尾，Alice都比Bob年长。一开始，Bob的速度很快，时间膨胀比较厉害，所以年龄增长比较慢。随着Bob的速度下降，其年龄增长速率又变得和Alice一样快；但是在返程途中，速度加快，所以年龄增长又变慢了。

Bob视角

在Bob看来，Alice是做一个反向的匀加速直线运动，并且运动的轨迹和时间与Alice看Bob似乎应该是一模一样的。按照费曼所说的"cocktail-party philosophers"的说法， “Oh, it is very simple: Einstein’s theory says all is relative!”。运动方式的确是相对的，那么计算出来似乎应该是Alice更年轻。问题出在哪里呢？在于隐含在背后的时空背景，即度规张量。

Bob视角下Alice的运动～Alice视角下Bob的运动（根据后面的计算可以看到，也并不是完全相等）

Bob视角下时空的样子!=Alice视角下时空的样子

采用Rindler坐标：

其中(T,X)是Bob感受到的坐标。它自己一直在这个坐标的1/a这个地方不动。这个坐标下的度规变成：

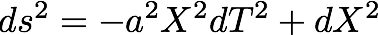
那么，Alice的运动轨迹就是：

这个轨迹显然就不是一条双曲线了：

注意到Bob视角里面是有一个视界的，X<0的地方是触碰不到的，一个粒子只能无限接近它但是不能穿过它。我们只能说，从分离到相遇这段时间内，Bob看Alice的确近似是一个匀加速的双曲运动，但是假如相遇之后Bob继续加速，把Alice甩在身后，他会看到Alice越走越慢，最后接近于停止在视界上。

从分离到相遇的时间很容易计算出来，是：

总时间和前面算出来的Bob年龄是一样的（换算成arcsinh就知道了）。下面计算Alice的年龄变化：

所以，在相遇的时候，Alice和Bob的年龄分别为

这和前面计算出来的结果是完全一样的，Bob还是比Alice年轻。

在Bob的视角下，整个过程中Alice年龄的变化为：

一开始，度规接近于Minkovski度规，可以按照普通的狭义相对论的时间膨胀来理解：Alice相对Bob在运动，所以年龄增长比较慢。但是，随着Alice跑到X比较大的地方，因为度规里面-a^2X^2dT^2这一项，Bob经历的一个小时间段内，Alice却经历了很长一段时间。所以蓝色曲线在中段，斜率迅速增大。正是这一部分弥补了佯谬，导致“虽然Alice相对Bob在运动，但是在Bob看来Alice的时间流逝更快”。

总结

孪生子佯谬中，Alice（惯性系）的视角：

Bob（非惯性系）的视角：

最终不产生任何矛盾。