【趣味数学题】 三角形的内接圆
郑涛 (Tao Steven Zheng) 著
【问题】
此问题选自会田安明(Aida Yasuaki,1747 年 - 1817 年)《算法天生法指南》(1811):
假设一个圆内接在一个边长为13、14、15的三角形中。问:内接圆的直径是多少?

【题解】
(1)用 “海伦公式” 或 秦九韶的 “三斜求积术” 公式 来计算三角形的面积。
海伦公式
海伦(Heron of Alexandria,约公元 10 年 - 70 年)在《度量论》(Metrica)卷一给出:
其中 为三角形的面积,
、
、
分别为三角形的边长和
为半周长(semi-perimeter)。
秦九绍的“三斜求积术”
秦九绍(1202—1261)在《数书九章》卷五“田域类”第二问给出:
其中 为三角形的面积,
为小斜边长,
为中斜边长,
为大斜边长。
(2)
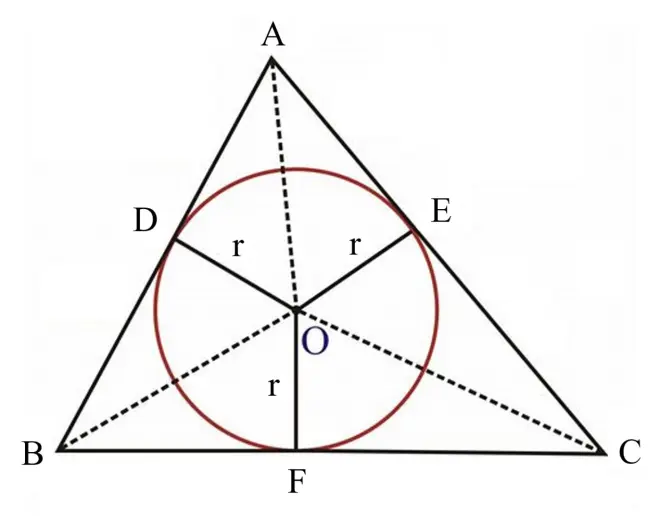
如图1所示, 可分为三个三角形:
,
and
。因此,
的面积是
其中
因为线段 、
、
都是圆的半径, 所以
。然后设
、
、
.
因此,
因为半径是直径的一半,
因此,内接圆的直径为

