散列函数一般设想：

首先，我们讨论什么是散列函数？

函数，就是映射，对应关系，对吧。散列函数也一样。我们设一个关键词为key，再设一个正整数素数m，让m去与key做模运算然后将他定义为散列函数h(key)，函数表达式为：h(key) ≡key(mod m)，他的含义是，函数h的值为key和m做取模运算，结果是key模m的最小正剩余。那么我们一开始说，函数就是映射，所以散列函数也不例外，这就是映射。我们把这种思想搬到程序设计上去，此时m是一个数组的容量，key模m的最小剩余为关键词key在m数组中的位置

例如m是111，key为64848212，那么h(64848212) ≡ 64848212 ≡ 1124 ≡ 14(mod 111)我们检测一下正确性：(64848212 - 14) 能够整除111，所以是对的。那么这个时候m数组中的第14的位置就存放着64848212这个数据。所以14对应着64848212所以是映射。（事实上这样算是错误的，我只是举个例子说明是什么样子的，下面会说明为什么错误）

另外，m不能是一个关键词key的基数低b的方幂。例如当关键词是十进制的时候，m不能是10的3次方。这是因为此时再做模运算，散列函数会简单的变成关键词的后几位数字，并且这可能导致关键词不会在数组中分布均匀，例如这样会让最后三位数字在000到099之间，很少会在900到999之间。类似的利用一个可以整除b^key ± a的数也是不明智的，其中key和a模m来说是较小的整数，在这种情况下，h(key)会强烈的依赖关键词的某几位数，并且相似的却重排了数字顺序的不同关键词可能会被发送到一个存储单元中。拿上个例子来说，若m = 111， 因为111整除(10^3 - 1) = 999，即10^3 ≡ 1(mod 111)所以64212848和64848212会被发送到一个存储地址，因为

h(64848212) ≡ 64848212 ≡ 1124 ≡ 14(mod 111)

h(648212848) ≡ 64212848 ≡ 1124 ≡ 14(mod 111)

所以他们两个都会存储在14这个位置。为了避免这种麻烦，应该找一个接近m的素数。像上面这种情况叫做冲突。下面是对于散列函数实现的代码演示

我们再谈论，解决冲突的方法

分离链接：

散列表，也可以看作一个线性表，借助线性表的思想，我们进行改进

其思想是，将散列冲突的元素保留在一个单链表中，这些表都有表头

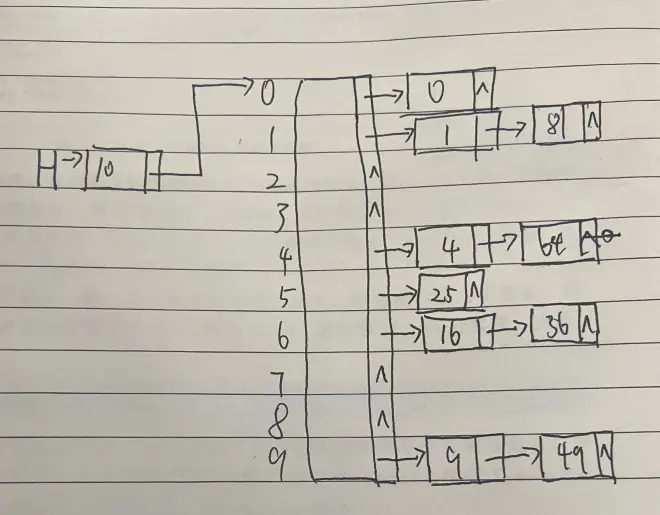
举例说明：假设关键字是前10个完全平方数并设散列函数就是h(X) = X(mod 10)(表的大小不是素数是为了简单起见)如下图所示

 以下是表的类型声明代码：

散列表初始化：

 散列表查找Find函数

插入操作

删除是链表中的删除操作直接实现，就不多赘述 

总结：分离链表的操作很像链表和栈的结合，另外这个insert函数计算了两次散列函数，多余的计算其实是没必要的。

当然，还有开放定址法，线性探测法（需要微积分知识），平方探测法等等