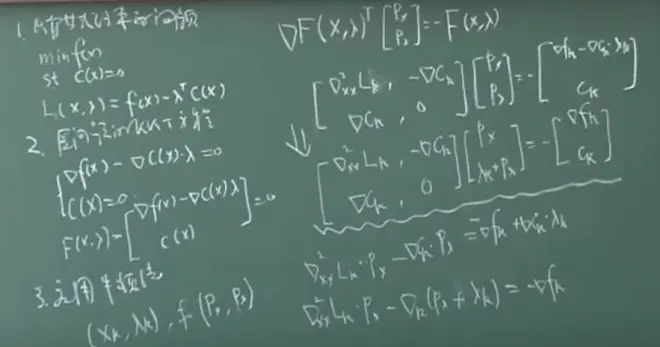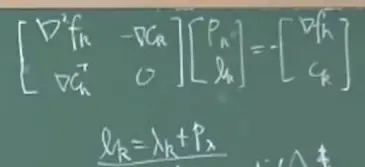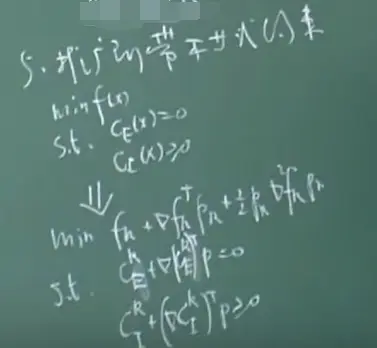数值优化 复旦大学吴立德教授

本笔记不关注证明过程
P2 无约束优化的基础
从初始点一步一步到最优点:
终止条件:


全局收敛:起始点x0任意,收敛到x*
局部收敛:x0∈N(x*) ,收敛到x*。(x0在解的附近)
线搜索方法:x0=xk,方向pk,步长αk,xk+1=xk+αkpk
选方向:
- 最速下降法:pk=-▽f(xk)
- 牛顿方向:pk=-▽^2 f(xk)^(-1)▽f(xk)

- 拟牛顿方向:pk=-Bk·▽f(xk)
- 共轭梯度法:
信赖域方法
在xk附近构造二次函数
P3 线搜索方法
φ(α) :=f(xk+αkpk)
方法:xk+1=xk+αkpk
最速下降:pk=-▽f(xk)
步长:αk=argmin φ(α) = argmin f(xk+αkpk)
wolfe条件是一种选取合适步长α的准则
保证下降得比较快
下图第二个不等式:忽略分母||pk||,左侧为曲线上任意一点与最左侧点连线的斜率,右侧为选定斜率,两斜率要满足不等式关系。
第一个不等式由第二个推导而来(个人猜测)。
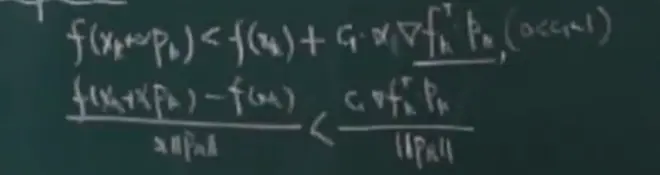
下面右图中加粗的段就是满足wolfe条件的区域,

保证步长α不会太小,取值在蓝色区域
下图第一个式子表明曲线上任意点的斜率应大于某值,这就让α的取值在平移后的蓝色直线的右侧,保证了α不会太小。
第二个式子左侧应右乘pk(应该是笔误了)


满足wolfe条件的α是存在的
此函数为关于α的函数φ。

P4 线搜索方法的收敛性和收敛速度

紫色区域比初始值小,其值f(x)称为下水平集
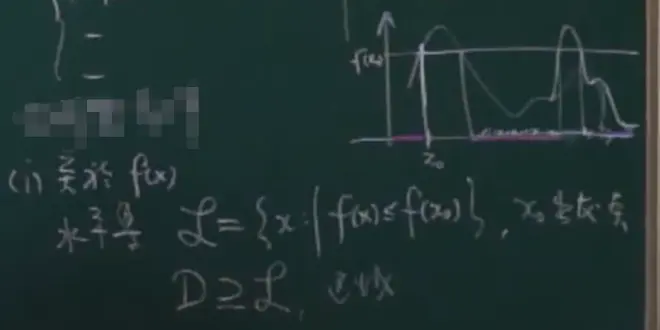
定理中的Σ<∞,也就是其中的每一项趋向于0
(L>0)


下图中λ为特征值,Κ为条件数

P5 算法收敛性
Zoutendijk定理加上以下条件,则拟牛顿法收敛。

下图第一行等式右侧第一项右上角缺-1


因为当xk离x*比较远时:
- 二阶梯度有可能不正定,方向也就不一定是下降方向
- αk不一定能满足wolfe条件
所以要对牛顿法进行修正

当上图中λi全为正,二阶梯度正定。
一般情况下不全为正,所以需要用其他矩阵来将λi变为正或者0
方法1,正数对应的位置为0,其他位置按λi'=ε-λi得出,但其中的矩阵不是对角阵。

方法2,把所有位置加上同一个λ,需要试探。
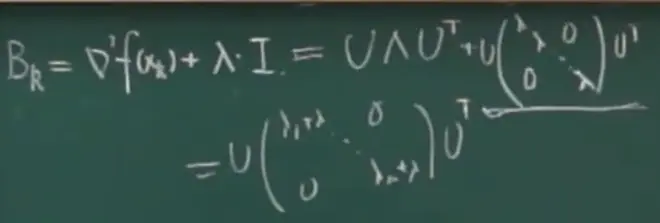
P6 正定矩阵的cholesky因子分解


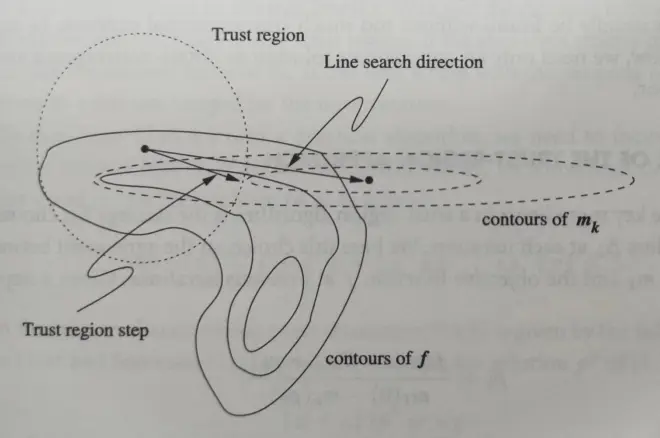
信赖域方法在当前的迭代定义一个区域,在此区域内能够相信(trust)模型可以充分代表目标函数。然后选择步(step)作为当前区域的近似极小值点。
如下图所示,尽管用到了最优步长,(基于模型)由线搜索方法找到的极小值点只会使f减小很小的一部分;而由信赖域方法找到的步则可以造成f的大大减少。(越靠近中心越小)
算法4.1
下图中的mk是f在xk的二阶泰勒展开,通过最小化mk求得p,用相应的p作为步迭代f。
ρ的分母一定是非负的。

根据ρ来选择信赖域范围Δk和xk

P7 基于Cauchy点的方法




- ||p(τ)||是τ的上升函数
- m(p(τ))是τ的下降函数
引理4.3

P8 定理4.5

P9 定理4.6
定理4.6





去优酷学习本讲。
P10 非线性共轭梯度法1
共轭梯度法最早是用于解由正定矩阵作为系数的线性方程组。
可作为高斯消除法的替代,而且能解大型(线性、非线性)方程组问题。
1、问题
问题①:解一个线性方程组问题。
问题②:二次规划问题
在求解问题②时,我们要找到x*,求f(x)的梯度可以得到问题①中的线性方程组,(不那么严谨的讲),零梯度为0可得x*。
上面的两个问题是等价的,这种等价可以让我们把共轭梯度法解释为:解线性系统的算法,或最小化凸二次方程的技巧。

2、共轭方向
(一对正交向量是关于单位向量的共轭向量)
{pk}是共轭方向组,其中的元素两两共轭。
下图中倒数第二行,因为正定矩阵的转置是其本身,所以等式成立。


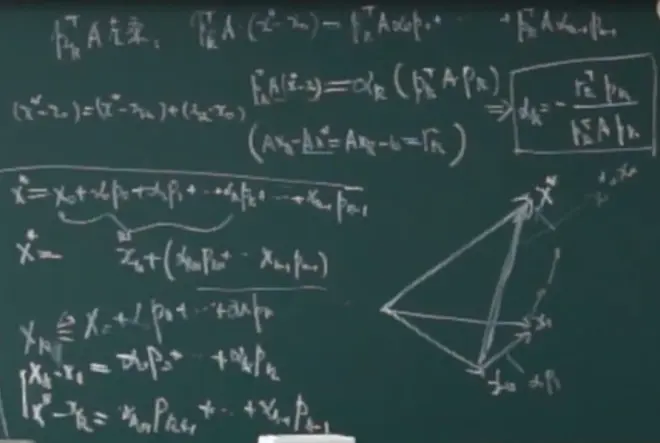
性质
αk=argmin f(xk+αkpk)
xk=x0+α0p0+......+αk-1pk-1
xk=argmin f(x0+u)
算法
xk、pk =>αk=argmin f(xk+αkpk) =>xk+1=xk+αkpk
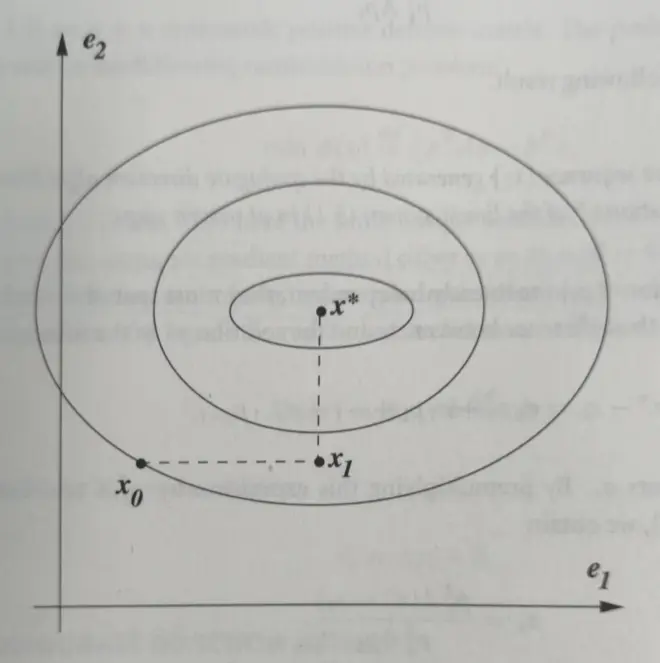
几何解释
在X空间中沿着pi变化,在Y空间中沿着某一轴变化
对于Φ(x)=Ax-b,当A是对角阵时,Φ的contour是一个长短轴与坐标系平行的椭圆,这样就可以沿着坐标轴方向寻找minimizer
3、共轭梯度法
性质ii说明构造的向量是共轭向量

以上方法可以用来①得到大型线性方程组的近似解②二次函数优化问题的渐进解
P11 非线性共轭梯度法2


引理5.6保证pk+1是下降方向
强wolfe条件的个人理解:k+1的斜率要更大



P12 拟牛顿法
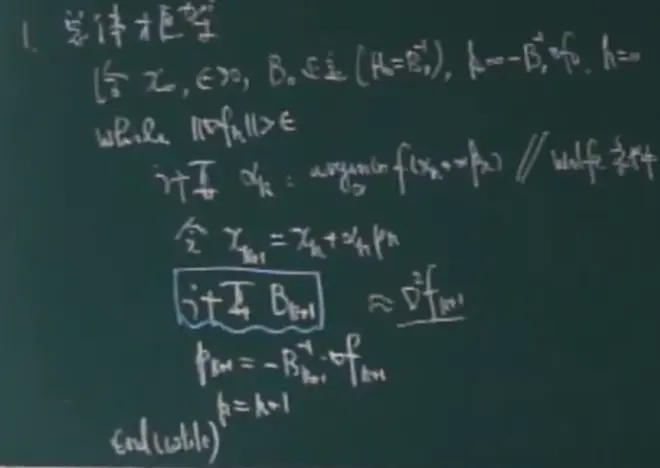

下面两种方法分别推导出通过梯度的差,x的差算Hk+1、Bk+1,用H、B算pk+1
①DFP方法


SR1:Symmetric Rank 1

①矩阵的迹
trace(A)△=Σaii,定义为主对角线元素之和
性质:trace(A+B)=trace(A)+trace(B)
trace(uuT)=trace(uTu)=||u||^2
trace(AB)=trace(BA)
trace(aA)=atrace(A)
trace(A)=Σλi(A) 矩阵特征根之和等于迹
②方阵的行列式
定义 det(A)=Σa1i1·a2i2·......·anin
性质 det(aA)=a^n det(A)
det(AB)=det(A)·det(B)
det(A)=Πλi(A) 特征根之迹等于行列式
det(I+xyT)=1+yTx
(A+B)^(-1) = B-1(A-1 + B-1)A-1
定义 A^(-1) 《==》det(A) /= 0
det(A-1)=1/det(A)
矩阵逆引理
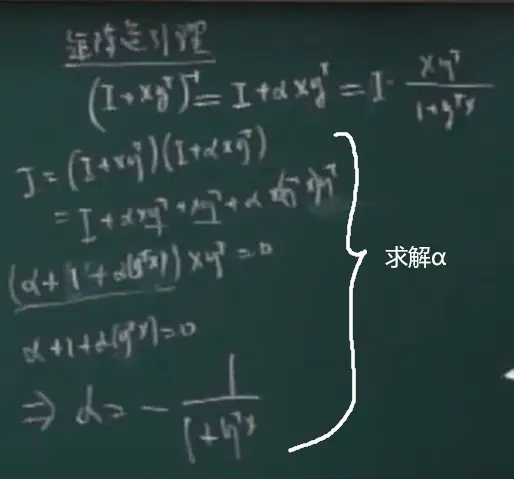
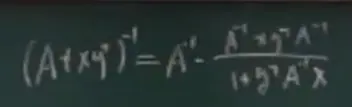
④Ψ(A)=trace(A)-ln det(A)
P13 BFGS方法

①曲率条件:
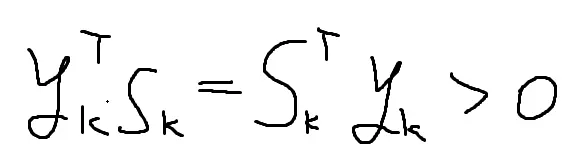
引理:如果pk是下降方向,且αk满足wolfe条件,则曲率条件成立。
引理(BFGS方法):如Bk正定,则Bk+1正定。
定理:
条件:nabla f(x)满足lipschitz连续,且
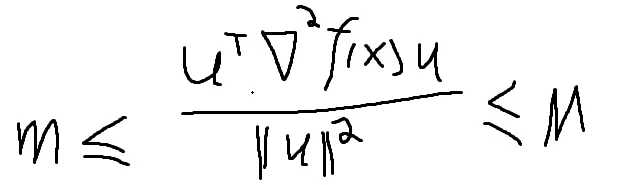
则:lim inf||fk|| = 0
P15 计算导数




P16 无需导数的优化方法(DFO)


坐标下降法:遍历n个坐标方向e1,e2,......en,轮流在每个方向进行线搜索以获得新迭代。
在第一次迭代中,固定除x1以外的其他x,找到能使目标函数最小(至少减少)的点;下一次迭代,固定除x2以外的其他x,进行搜索。

上图为包含两个变量的二次函数利用坐标搜索方法进行优化。



在传统的共轭梯度法中要通过导数来获得共轭向量。
为了不用导数,用{e1,e2,...en}构造一个线性子空间,f在S1,S2中的最优解x1*,x2*组成的向量x1*-x2*与{e1,e2,...,en}共轭(线性子空间性质)。f在S1中求最优解x1的问题可以变为在S中求最优解{c1,c2,...,cn}的问题,而此问题可化为对单个c求解的问题(上图最后一行)。

又称单纯形法。
n维空间中的n+1个点可以构成一个单纯形,如下图右侧所示。

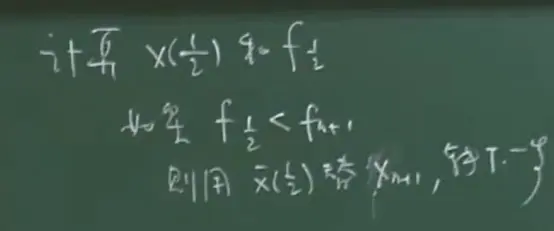

P17 最小二乘方问题
用下图第一行的式子来衡量模型和系统的观测之间的差异。

下图中的rj(x)是一个对从x1到xn的偏导组成的向量。




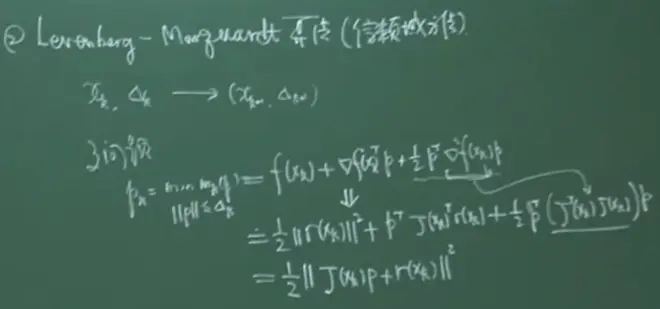

P18 非线性方程组



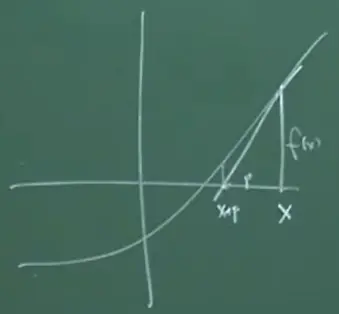





H(x(s)),λ(s))=0
求H全微分:
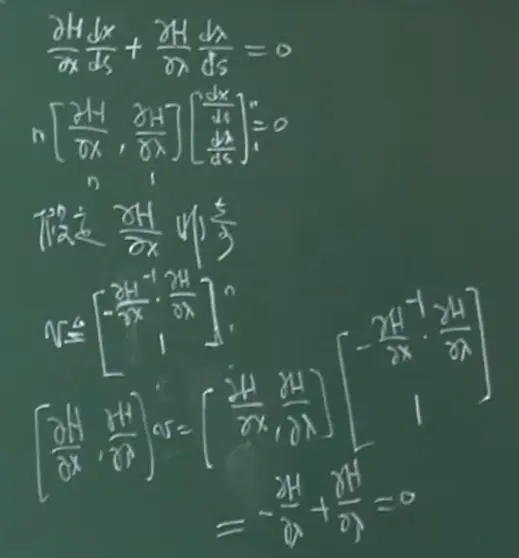
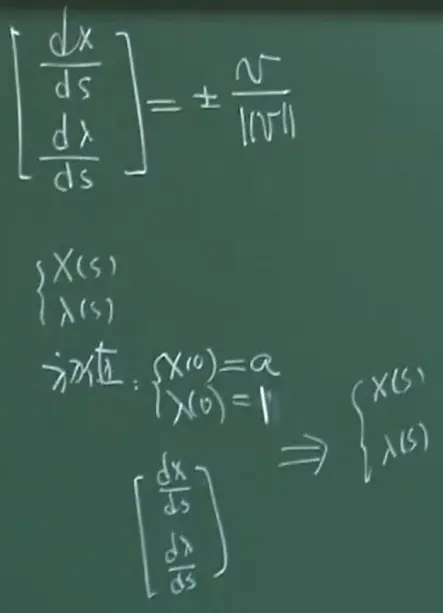
P19 约束优化理论

积极约束集:在不等式约束中,当x给定后,ci(x)可以分为两种,其中ci(x)=0的部分包含于积极约束集。


约束问题的lagrange函数
用拉格朗日乘数法解决只有等式约束的问题。分别对每个x求偏导。
用KKT条件求包含等式和不等式约束的问题。

对偶理论表明我们可以从原有的优化问题中,利用其函数与数据,构造一个alternative问题。
本小结的结论都是在下面的情况下得出的:

即无等式约束,目标函数和-ci(x)都是凸函数。
下图中不等式约束前的λ>0。

对偶函数:max θD(λ)
s.t. λi大于等于0,i∈I
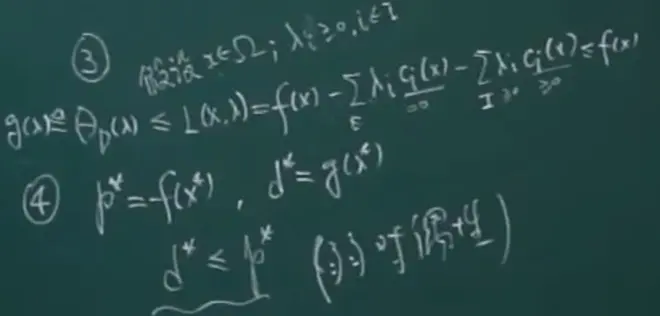


P20 基本的必要条件
x是解的必要条件


如果积极约束都是线性函数的话,也就是A(x)内都是线性函数


P21 点与凸集的分割定理


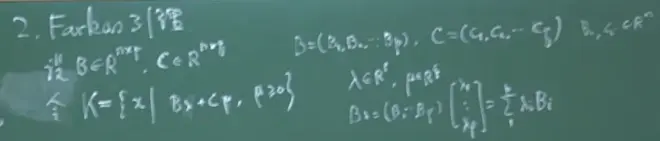

λ∈R^p
K是闭凸集

定理(强对偶成立条件)
min f(x)
s.t. ci(x)≥0, i∈I
且f(x), -ci(x)都是凸函数,kkt条件成立
则强对偶性成立
P22 SQP方法和内点方法

序列二次规划sequence quadratic programming