Definition of the maximal Lyapunov exponent

在Logistic模型中，有如下典型结果图示：

不难注意到，图像每个极大值点对应于一个倍周期分叉点，可利用这个特征来进行分叉位置的求解。

此结论未能找到证明，不过可以在自适应算法的迭代过程中，通过图像验证是否为分叉位置。

观察代码运行的结果，可以发现每两个分叉点之间的图像具有非常良好的相似性质。

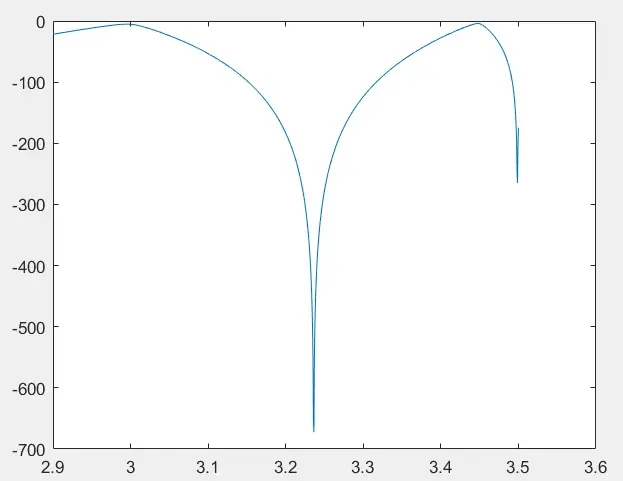
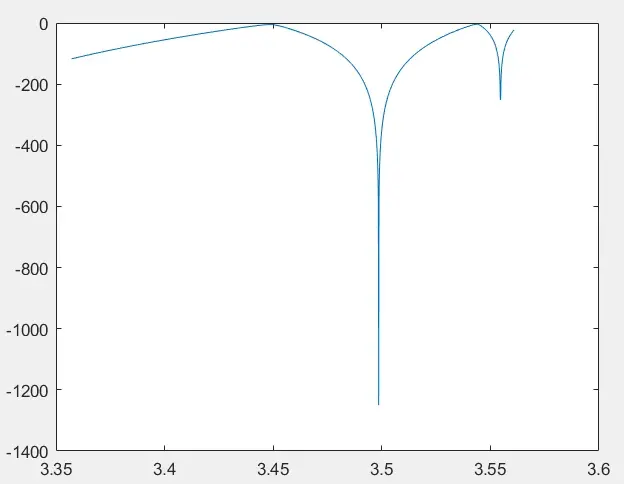
这启示作者可以采用自适应算法，在每次循环计算过程中只寻找两个分叉点，然后缩小并更新下阶段的计算区间，加大计算精度和Logistic模型的迭代次数。

关于自适应算法，由于每次倍周期都会在原先的周期数上乘2，故而为保证精度迭代次数应选取倍周期的倍数，T=T0*2^i；而对于每个区间的采样数，本文采用了线性递增函数。这部分算法读者可以进一步优化，从而提高计算速度和精确度。

以下是Matlab代码：

clear;clc;

format long

tic

%% 初始化

x=0.5;y=0;

N=1000;

u=linspace(2.9,3.5,N);

T=200;

U=[];

%% 自适应计算

i=1;

while i<13

    for j=1:T

        x=u.*(x-x.^2);

        df=log(abs(u-2.*u.*x));

        y=y+df; %计算Lyapunov指数

    end 

    % plot(u,y) 作图观察

    [val,idx]=findpeaks(y); %寻找分叉点

    u1=u(idx(1));u2=u(idx(2));

    U=[U(1:end-1),u1,u2];

    

    T=T*2; %自适应算法，可以进一步优化

    N=N+500;

    u=linspace((4*u2+u1)/5,(5*u2-u1)/4,N);

    

    x=0.5;y=0; %进入下次迭代

    i=i+1; 

end

%% 数据处理

for j=1:length(U)-1

    mu(j)=U(j+1)-U(j);

end

for k=1:length(mu)-1

    Lya(k)=mu(k)/mu(k+1);

end

plot(1:length(Lya),Lya)

toc

代码运行结果：