【2023福建高三质检数学】2023年度虐心大戏——福建省质检数学试卷解析！

我对福建省检21题的一些看法与见解：

其实21题这种类型是妥妥的非对称韦达定理，太经典了。

如果你知道模型，就一定知道Q的轨迹是一条和x轴垂直的直线，很快就可以判断

过椭圆焦点的直线与椭圆交于两点，这两点又和左右顶点连线交于另一点，那么这个交点在定直线上（x=m)

2020年全国一卷圆锥曲线用到了几乎一模一样的模型，只不过这次给出了定直线。需要我们反过来求直线过定点。

这类题型在模拟题里面也是屡见不鲜

解决这类非对称韦达定理的方法也很多，比如：

（1）需要涉及极点和极线，不过这种方法可以说华而不实，如果不追求130分以上真的没有必要知道什么是极点极线。

（2）主流方法就是设直线，与椭圆联立，然后写出韦达定理公式（这一步基本属于套路）

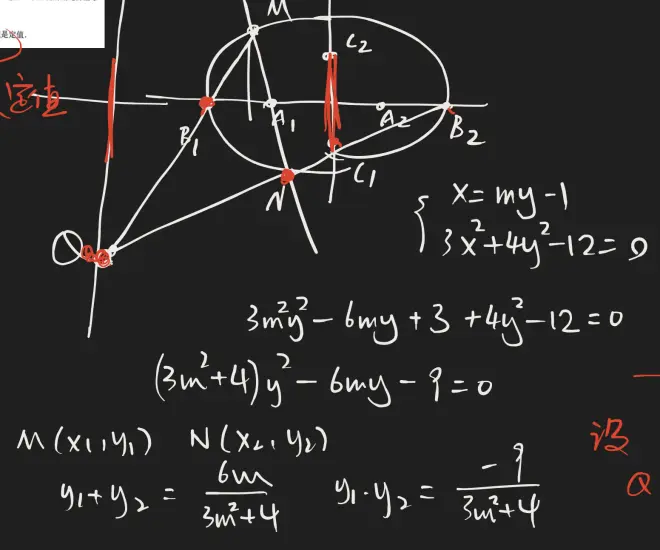
然后我们可以设交点坐标，然后运用相似把已知的坐标关系全部表示出来

随后整理一下形式，

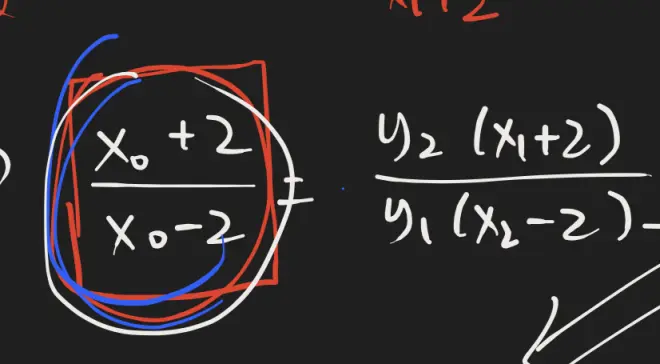
这里面其实也需要一些小技巧，因为我们内心清楚其实点在x轴定直线上(x=m)，但是不好明说，所以我们这样转化一下。

然后来到了整个方法的核心，把椭圆方程改写一下在反代入我们得到的非对称韦达定理式

进行消元后，我们就可以得到正常的韦达定理式，也就可以运用韦达定理来继续做了

同样地，2020年全国一卷也可以用这种方法做

基本上这样做可以解决绝大部分非对称韦达定理的题目，如果还有更好的做法也欢迎补充。