地球发射入轨弹道设计基础(for KSP-RO)
地球发射入轨弹道设计基础
—— Kerbinator 利用 KSP+RSS+RO的研究
( 甚至可以是真实的火箭,尽管有些不太现实 )
来自作者的善意提醒:
*你可能没有足够的钱来建造一个(笑),但你仍然可以在模拟中完成它!
**这篇文章不包括火箭制导单元中的实际PID回路控制编程,但它确实给出了正确的上升俯仰程序。您可以编写kOS脚本(在KSP-RSS-RO中)以提高精度。此外,这篇文章不是非常定量的,它只写在定性层面,因为它无法使用算法精确计算精确的最佳优化轨迹;要为特定的火箭制定正确的俯仰程序,你应该按照我的指示,模拟5-10次,直到你的轨迹完全优化,也就是说,你的第一级俯仰偏离前进方向的角度不要超过5度,你的第二级可以有一个静态俯仰,一直到低轨轨道,其远点和近点之差不超过50公里,近点高于140(160)公里。
关键词:地球轨道, 上升轨道, TWR , SLT , delta-v , Isp
现实的火箭可以将轻或重的有效载荷输送到不同的轨道,而初轨道,也就是说这些航天器直接进入的第一个轨道通常是近地轨道(LEO)或地球静止转移轨道(GTO)。然而,有效载荷质量对火箭结构和上升弹道有很大影响。这里我们只关注两级火箭的上升弹道,我将分两部分来解释,理论和例子。第一部分我将解释理论,第二部分我将提供一些例子来说明它是如何工作的。
这里的主要理论因素是TWR、delta-v和Isp。首先,TWR(或SLT)显示了飞船对抗重力的能力。随着TWR的提高,你将能够更快地上升并轻松获得更高的垂直速度。所以这就是为什么第一级通常具有1.2至1.5的高SLT,基本上是因为它们垂直升空,推力必须克服重力,所以TWR必须高于1,但如果你不想在发射开始时损失大量Δv,随着你不断消耗燃料,飞船变得更轻,但由于发动机结构不可改变,推力丝毫没有降低,你的TWR将大大增加,通常在MECO达到6-7。我还想指出,峰值G力对宇航员和航天器(尤其是前者)是有影响的,所以即使是土星五号的SLT也很差,只有1.13,但就在MECO之前,他们在MECO前几秒钟关闭了一台F-1发动机,但这实际上并不会降低其效率,因为如果TWR超过4,则几乎没有差别——重力几乎可以忽略不计。(太高的)TWR也会影响火箭的效率,因为TWR越高,发动机的结构质量就越高,更高的结构质量意味着delta-v的降低,因为你会得到更高的起始质量和更高的终止质量,所以dv会降低。此外,HLV的一个有趣之处是,它们通常具有非常低的初始TWR,只有大约1.1-1.2。这是因为,首先,推进剂比发动机便宜得多,因此,这可以被视为一种具有额外燃料的高SLT火箭,有助于它获得一定的速度和高度。更重要的是,它以相对较低的速度离开稠密的低层大气,可以降低施加在火箭头部的动压,保护火箭不因空气动力而像挑战者号航天飞机的轨道器之类的被撕裂。同时,它还可以防止在MECO之前出现极高的重力峰值。但一些MLV,如阿特拉斯551和德尔塔II/Delta IV M,并不遵循这一规则——它们通常通过使用安装在侧面的一些小型固体火箭助推器来实现良好的起飞TWR,以帮助第一级从地表以足够的速度起飞冲上天空。尽管固体火箭助推器的Isp比液体燃料发动机的Isp低,但由于其重力损失比低TWR火箭低,因此仍然提高了效率。更先进的解决方案是CBC设计,用于Delta IV重型和Falcon重型火箭,使用三个平行的相同大型液体燃料助推器,中央核心节流阀降低,使其在两侧助推器后燃烧。
第二个因素是Δv。尽管Δv不是净速度变化,但它与考虑计算重力损失的(净)速度变化量直接相关,特别是(取决于)MECO速度。MECO速度决定了第二级的最低初始TWR。例如,如果MECO速度仅为2.7 km/s左右,如SpaceX Falcon Heavy,第二级TWR必须至少为0.9,但如果你的MECO速度是4.3km/s,就像大多数真正的HLV一样,你就可以将第二级的TWR降低到0.36。这是因为MECO速度越大,第二级绕轨道运行所需的时间就越短(同一推重比下),因此重力损失也就越小。从另一个角度来看,第一级的水平速度越快,第二级获得的离心力越大,第二级受到的重力拉力就越小。因此,尽管只有1.5km/s的速度差,仅为delta-v总消耗量的18%,但第二级的所需初始TWR却存在巨大差异。
第三个因素是Isp。这不是上升弹道的一个主要因素,但它以一种特殊的方式影响上升弹道。这是因为,在相同的推力下,如果Isp更高,你将获得更低的推进剂通量,TWR的增加将更慢。例如,起始TWR为0.3,相同的6000 delta-v,让我们比较液氢NTR(1200s Isp)级和UDMH-NTO(300s Isp)化学火箭之间的质量变化。参考火箭方程:delta-v=Isp*ln(mi/mf),其中mi和mf代表初始和最终质量,如果它们一开始都是500t和0.3TWR,让我们假设地球G为10m/s2,因此,NTR级的最终质量为303.265t(=500/e^0.5),LH2 LOx级的最终重量为67.67t(=500m/e^2)。因此,最终TWR为0.4946和2.216,平均TWR分别为0.385和0.815,这是一个非常大的差异。因此,如果你使用的是D4H方法(我将在后面提到),当向东发射时,如果你用的是初始TWR 0.28的LH2-LOx上面级,你的GTO轨道的长轴将与你的发射点与地球中心成60°角,但如果你使用的是氢NTR上面级,初始TWR也为0.28,角度将变为90°。
我已经建造了三艘假想的火箭,我将以它们为例。实际上,第一艘是典型的LLV,第二艘是专门设计的HLV而缺乏现实生活中的对应物,第三艘主要是为了特殊需要,将飞船直接注入高能轨道,其设计比真正的Delta IV重型要激进得多。
第一个是QueQiao LV,这是一种典型的轻型运载火箭。它被设计为携带750公斤左右的有效载荷到TLI。它还有一个单独的第三级火箭发动机,用于在到达LEO后一段时间燃烧TLI,因此计及TLI火箭发动机的质量,其LEO有效载荷约为2.1吨,我们只关注LEO上升部分。
在该火箭的设计中,由于历史上完全缺乏200kN级的地面优化发动机,我使用了一台真空发动机(俄制RD-0124,1990年代),它在真空中提供了良好的359s Isp,但在海平面上提供了中等的245s Isp(245s海平面Isp比地表优化的发动机差得多:地表优化的发动机大约为302s,但比大多数真空优化发动机好得多,因为大多数真空优化发动机在海平面的Isp低于200s,这太差了,无法使用)。所以我选择了西昌发射中心,它的高度很高,Isp和SLT都大大增加,比在同一纬度但海拔低很多的卡角发射效率更高,这要归功于更高的Isp(更高的delta-v)以及更高的SLT(更低的重力损失)。
事实上,这种火箭的TWR相当高,因为Isp和推力都随着高度的快速增加而增加,因此助推器和芯一级的最终加速度都非常高,都高达7G。
第二级TWR也很高(0.8是令人惊讶地高,除了SpaceX的Falcon Heavy,因为MECO速度太低,只有3km/s的地表速度)。这是因为所有发动机都有较大推力,而S1.5400/RD-58系列的Isp非常高,2000年左右的RD-58M-CCN达到了惊人的361s,而普通液氧煤油发动机,真空机通常具有340-345s的真空Isp,而高级的地面机通常为336-338s。
因此,轨道变成了一条连续上升的曲线,在轨道插入点的末端变得非常平坦。下面是上升曲线:对于第一阶段,以100m/s的速度将速度矢量调高到高于地平线85度,然后跟随速度顺向prograde向上或向下调1-2度,使得700m/s时速度矢量相对于地平线向上为45度,助推器分离时为25度,然后在助推器分离时尽量取得700m/s的上升率,当速度矢量下降到地平线10度以下时,向上俯仰一点。这样,你将精确控制MECO时上升率为460-470m/s。然后继续推进,直到地表速度达到6.2km/s时下降率降低到20m/s以下。然后俯仰3度左右,使垂直速度始终精确为零。然后,你将进入141-160km的圆形轨道。
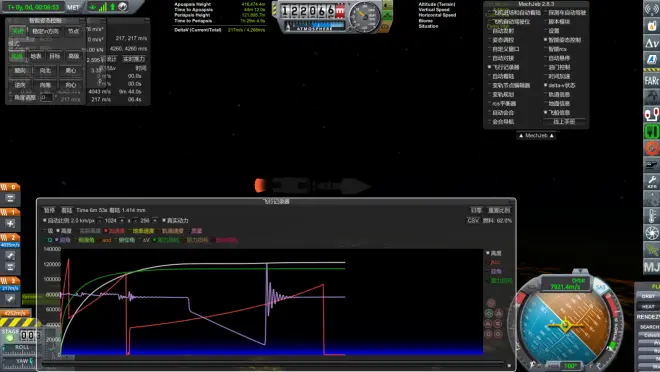
*紫色线表示船的迎角的垂直部分。
下一个,Moon Odyssy HLV,是一种重型先进火箭,用于运载一个无对接的5吨月球着陆器。(*注意,甲烷为燃料的固体核心核推的Isp是不现实的;实际Isp可能在500s左右,这听起来不是好消息,因为甲烷的效率仅为LH2的1/2.828,但带有LOx补燃的LH2核推具有类似的推进剂密度和Isp,可以作为替代品。这实际上是模拟中的错误)
我使用了一个半假想的RO Raptor(Surface Variant)发动机(中使用了埃隆·马斯克的会议的某3500kN的PPT信息),甲烷核推作为第二阶段。
由于第二级点火TWR相当低,而第一级dv也不够(第二级效率远高于第一级,因为它的Isp高得多,所以增加其(在总dv中的)占比)。因此S2上升相当困难。
另一件恼人的事情是,S1的SLT也很差,只有1.18。这在许多重型运载火箭中很常见,比如土星五号,其SLT极低,1.13,在上升开始时,几乎88%的dv都被重力抵消,当它从发射台缓慢上升时,会造成巨大的重力损失。然而,添加更多的燃料实际上比增加发动机便宜得多。如此低的TWR主要是出于经济原因。
因此,这里的策略是在开始时轻轻转弯。这枚火箭的上升曲线如下:我以40、70、130m/s的速度一个接一个地转弯3度,这样它的地表速度在100m/s时恰好指向85度。从那时起,只需保持它在速度顺向prograde上仰1度,这样即使由于地平线上的仰角降低使得200-500m/s时重力转弯速度变得非常快,它仍然能够在地速1000m/s时保持其相对于地平线45度的俯仰,这是一个重要的检查点。
然后,我将在地速3.2km/s是达到MECO,在300km高度达到170km的远点。因此,这艘船将有一个非常大的垂直速度,超过1km/s,以帮助低TWR的2级通过消耗垂直速度对抗重力,并获得足够的圆轨时间。
然而,仅使用第1级的垂直速度是不够的。因此,第2级仍需要大量抬头,以保持高度,防止飞船坠落过快,并因大气严重过热而导致剧烈爆炸。我从实验中得出,对于在约310km进入低轨来说,(相对于速度顺向prograde)28度抬头几乎是完美的,当上升过程中达到的最大高度为350km时,该船实际上在到达Ap后很长一段时间才进入了低轨轨道。这纯粹是因为第2阶段的低TWR:像这样的飞行器不可能在到Ap之前以如此小的1级dv和二级推重比直接圆轨。在这里坠落并不重要,飞船仍然远离大气层。(然而,这对于载人任务来说会出现一个”小”问题:如果发动机因意外而失效,任务被迫中止,飞船将进入高亚轨道再入,这将产生一个极端的G力峰值:现实历史的苏联Soyoz 18a由于发射失败而中止,因此它在192km Ap的亚轨道进入大气层,而G的峰值已经有惊人的23G,这给宇航员带来了生理不适;如果Ap是280km,正如我在该飞船的猛禽发动机回收过程中测试的那样,峰值重力将超过40G,持续约10秒,足以杀死宇航员;幸运的是,目前大多数发动机都非常可靠)

图2 Moon Odyssey HLV的遥测数据(aod表示飞船垂直部分的绝对攻角)
注意,随着时间的推移,aod会有一些变化,因为我是在Smart A.S.S的帮助下手动控制它,而我使用的aod(大约28度)是一个实验值,并不精确
更激进的方法是D4H-Ex(超过ULA的Delta IV Heavy)上升弹道(仅用于货运任务;出于与上述相同的原因,我估计任务中止后的最大减速G-Force将超过100G,将可怜的宇航员压成薄饼并导致立即死亡),其目的是在不进入低地球轨道的情况下直接注入GTO。一级会大幅度抬头,同时让火箭达到极高的远点和极高的上升率,然后第二级将只较小抬头(速度顺向Prograde向上约10度)并燃烧较长时间,最后直接进入大椭圆轨道,如地球静止转移轨道(GTO)或地月转移(TLI)。在这种方法中,不可能注入低地球轨道,但可以使用非常低第二级TWR,低至0.28(这个值几乎是固定的,因为我的实验得出了这个值,0.29会使Pe过高,0.27会进入大气层并烧毁,导致灾难性失败)。如果您使用NTR,它将非常好,因为NTR非常重且高效,这意味着NTR(Isp 622s)所需的7500 m/s并不太多,但它在化学阶段(Isp 320-460)中这个dv是极高的。因此,它通过在核推级上堆积更多的delta-v来最大化核推级的高效率,所需的低TWR意味着它需要更少的核发动机,因此它具有更少的自重,因此效率更高。至于历史上的运载火箭,它们不使用核发动机,但也使用高能氢氧上面级,与大多数推进剂的300-330秒Isp相比,它提供了出色的460秒Isp。主要缺点是发射时间必须精调,因为与离开LEO不同,LEO可以让你的长轴指向任何你想要的地方,然而,在这个上升弹道中,它是由发射时间决定的。因此,月球起飞窗口从每天2个限制到每月2个。此外,发动机必须非常可靠,适合RL-10系列或NTR等长时间燃烧,以便在长得离谱的入轨燃烧过程中不会发生中途故障。
D4H上升弹道背后的原理相对简单:当你的速度高于该高度的圆轨道速度(7.6~7.8km/s)时,离心力将超过重力,下降速度将迅速下降。因此,很大的下降率并不重要;事实上,下降率峰值约为-1.2km/s,远高于俯仰上升以保持高度的方法的下降率,其中当初始TWR为0.45(我的实验值,使用核推)时,最大下降速度不能超过500m/s,这是俯仰上升方法可用的最低实际TWR。
先前在简单火箭1已经做过初试验,结果如下:
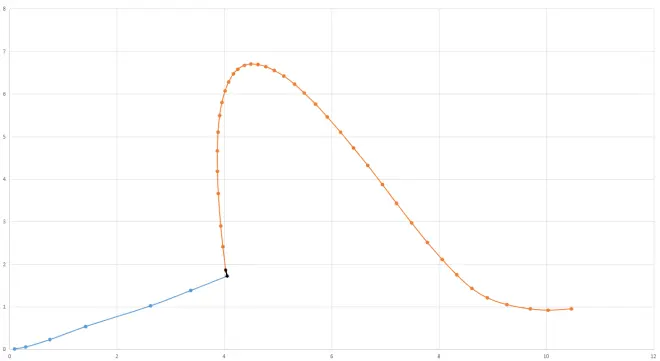
横轴为速度,单位km/s,纵轴高度,单位百km
因此,我使用了一艘飞船Lunacy(RF,而不是RO,这意味着这些发动机尽管具有近似现实的性能,但仍然是假想的)。在这个模拟中,弹道方案是,在MECO时保持速度升角为30°左右,并保持相对于速度顺向Prograde上仰10°。整个TLI上升的总dv为13.1km/s,远高于普通火箭的12.2km/s,然而,更少的发动机在相同质量下提供更多dv,更少的引擎意味着更低的总成本,这符合火箭设计的最终目标。曲线中的最高点是850km。
因此,这些是我的LEO/GTO上升弹道的一些部分,并且由于我使用了一整套拟真mods,所以结果非常可信,这可能适用于使用相同发动机和类似油箱的真实发射。这些计算机模拟可以节省大量时间,同时保持极高的准确性。它还提供了一种学习火箭技术的方法,而无需拥有类似SpaceX的公司。因此,在进行粗略估计时,它可以用于指导火箭设计。
我还想展示,这种方法是可靠的,因为所有结果在任何现实模拟中都是完全可重复的(特别是KSP-RO,我在那里开发了这些假设火箭:在没有发动机故障的情况下,QueQiao LV的成功率超过80%,而Moon Odyssey只有手动控制,成功率超过50%(没有自动驾驶,但我使用了智能驾驶辅助系统,需要手动控制作为数字输入)
现在我们已经梳理了低地球轨道上升轨道设计的基础:首先我们需要有9.0-9.6km/s的delta-v,然后我们将根据火箭的级TWR设计其上升剖面,然后在模拟中手动飞行,以优化您的轨迹,最后,如果第一级能够正确飞行,将船舶送至所需的高度和速度,而不会因前进而产生太大的俯仰,那么重力转向就可以了,最后,当你将第二级以一定角度俯仰时,它将在160公里以上的高度进入一个近乎完美的环绕地球的圆形轨道,你的设计将成功完成。
作者:Kerbinator
用时:121+184+114+62=481min;翻译为中文+50min
20191101 07:54于Kerbin University of Aeronautics and Astronautics(KUAA)(笑)

关于实用的弹道设计标准(二级)
MECO速度 - 二级初始TWR - 抬头角
2800 - 0.96 - 6°
3600 - 0.5 - 20°
4300 - 0.38 - 45°
0.38是低推重比二级的极限,再低的推重比,抬头维持高度法将不再适用。
全部为Ap后圆轨,MECO速度越高,二级推重比越低,掉高度越严重。
对于核推+普通抬头圆轨法:
TWR增长太慢,0.38需要修正到0.46,核推二级不建议过低的MECO速度。
坠落圆轨弹道推重比固定0.29-0.33:
坠落圆轨弹道需要高比冲长时间工作的上面级(弹道适应性);
更高的推重比会在高处提前Pe出地面,更低的推重比会坠毁。

原始文本展示
原始文本展示如下(其实是大一的英语写作作业(笑))
注:无修正。图片和上面的翻译展示版相同,已经略去。
THIS IS APPENDIX , NOT A PART OF THE ESSAY ! BY READING THIS APPENDIX YOU WILL MEET THE BASIC STANDARD TO READ THIS PASSAGE.
And this passage is written in a textbook/tutorial style.
* Small characters are used to fit the ultra-long passage into a small place huh.
Author:有道翻译勉强能看(有些地方写得还挺顺的)
A harsh 4h work!--As a part of my planned《introduction to aeronautics and astronautics for KSP-RO players》(←航概 for KSP-RO)
abbreviations:
deg/d:degree(s) (angle)
s1 , s2 ... : stage 1 , stage 2 , ...
LEO:Low Earth Orbit , 7728.3 m/s at 302.774 km alt ( typical for HLVs ); 7815 m/s at 160 km or 7824.5 m/s at 140.000km ( typical for LLVs )
LLV : light launch vehicle
HLV : heavy launch vehicle
TWR : thrust-to-weight ratio
Dv/Delta-v : the velocity change in total(not for net velocity change , considering steering losses , gravity losses , and change of reference frame) . It's the net velocity change when there is completely no gravity and the vessel is keep thrusting prograde , so in simulation you can cheat to set the gravity to zero in order to test your delta-v .
Prograde / retrograde:velocity vector's positive&negative direction .
Apoapsis : the farthest point of orbit from center celestial body (Earth , shown here ) . In suborbital trajectories , the ship ascend before apoapsis , and descend after apoapsis .
Statement : Well , despite being a modified video game , the Kerbal Space Program with Real Solar System , Realism Overhaul and Principia have a very realistic output in term of accuracy(provided by Principia’s N-body physics and FAR’s aerodynamic model ) and how things work(provided by Realism Overhaul) , similar to Orbiter , another video game ( really !) used by NASA scientists to calculate trajectories . Also KSP-RSS-RO is capable to do every real space mission so the output is realistic and plausible .
LEO : Low Earth Orbit
GTO : Geostationary/Geosynchronous Transfer Orbit
TLI : Trans-Lunar Injection
LH2 : liquid hydrogen( a kind of rocket propellant )
LOx : liquid oxygen( rocket propellant )
Isp : Specific impulse , which means impulse ( force * time ) the rocket gets with 1 mass unit of fuel(ex. a engine consume 1 kg of LH2 / LOx propellant and get a 1 t vessel accelerated 4.66 m/s , then its Isp is 4660 m/s , and after being divided by Earth G 9.80665m/s2 in British units , it became 474s )
Lunacy *: not * being mad * , this is my name on one of my ship as an attempt to a moon return mission carrying a 140-kg kerbal .
PLEASE read the abbreviation vocabulary first !
Author’s notes:
The first passage ( Introduction to Rocket Propulsion Technology ) is merely a collection of existing knowledge I learned from Wikipedia a year ago , but this is really my original work based on my own simulation experience , and it is quite simple (?) in comparison with those long essays , and is it far more general , not limited to specific rocket with a fixed ascent profile suiting its TWR and other properties .
IF YOU HAVE DIFFICULTY READING THE PASSAGE , PLEASE TAKE A LOOK AT THOSE PICTURES , AND TRY TO UNDERSTAND EVERY LINE IN THEM !!! IF YOU WANT TO FULLY UNDERSTAND THIS PASSAGE , PLEASE CONTROL THE ROCKET MANUALLY FOLLOWING MY INSTRUCTIONS !!!
Fig. A brief explanation of thrust ( right ) and gimbal ( left ) used for rocket control .
Earth Orbit Ascent Guidance for Realistic Rockets
(地球发射入轨弹道设计基础)
—— Kerbinator’s Research with Kerbal Space Program + Real Solar System + Realism Overhaul + Historical Rockets Parts Pack
( and hopefully , realistic rockets despite some inaccessiblities )
Author’s kind reminders:
* You may not have enough money to build one :D , but you can still do it in simulation!
** This passage does not include the actual PID loop control programming in rocket guidance unit , but it indeed gives out a correct ascent pitch program . You can write kOS scripts ( in KSP-RSS-RO ) to aim for accuracy . Also this passage is not very quantitative , it is only written to a qualitative level since it cannot precisely calculate the exact best-optimized trajectory using algorithms ;to figure the right pitch program for a specific rocket , you should follow my instruction and simulating is for 5-10 times until your trajectory is fully optimized , that is to say , your 1st stage don’t pitch out of prograde for more than 5 degrees , and your 2nd stage can have a static pitch all the way to a LEO orbit whose difference between apoapsis and periapsis is no greater than 50km and periapsis is higher than 140(160)km.
Keywords : Earth orbit , ascent trajectory , TWR , SLT , delta-v , Isp
Rockets in reality can deliver a light or heavy payload to various orbits , and the primary orbit , which means the first orbit these spacecrafts directly inserts in is usually low earth orbit(LEO) or geostationary transfer orbit(GTO) . However the payload mass affect rocket structure and ascent profiles a lot . Here we’ll only focus on the ascent profile of two-stage rockets , and I’ll explain it in two parts , theories and examples . In the first part I’ll explain theories and in the second part I’ll provide some examples which shows how it work .
The major theoretical factors here are TWR , delta-v and Isp . Firstly , TWR( or SLT ) shows the ship’s ability to fight against gravity . With a higher TWR , you will be able to ascend faster and gain more vertical speed with ease . So this is why the first stage usually have a high SLT of 1.2 to 1.5 , basically because they lift off vertically and thrust have to overcome gravity force so the TWR must be higher than 1 , but if you don’t want to lose a large amount of delta-v at the beginning of launch , you will have to get your SLT at least 1.1 . For instance , if your SLT is 1.2 , that means you will lose 80% of your delta-v due to gravity pull . However , as you consume fuel constantly the ship gets lighter but thrust does not decrease at all due to unchangeable engine structure , your TWR will increase a lot , and typically hit 6-7 at MECO . I also want to point out high peak G-Force is brutal to astronauts and spacecrafts , so even the Saturn V has a poor SLT of 1.13 , but its TWR just before MECO is so high that to make astronauts comfortable , they turn off one F-1 engine seconds before MECO , but this does not actually decreases its efficiency , since there is nearly no difference if TWR goes over 4——gravity become roughly a negligible factor . TWR also affects the rockets’ efficiency since the higher your TWR get , the higher the engine’s structural mass will become , and a higher structural mass means a decrease in delta-v since you will get a slightly higher start mass and a much higher terminal mass , so dv decreases . Also , an interesting thing about HLVs is that they usually have a very low initial TWR , only about 1.1-1.2 . This is because , firstly , propellant is far cheaper than engines , so this can be viewed as a high SLT rocket with extra fuel which help it to gain some speed and a lot of altitude . What’s more it goes out of dense lower atmosphere with a relatively low speed and it can lower the aerodynamic pressure exerted on the nose of the rocket , protecting rocket from being torn up due to aerodynamic forces like space shuttle challenger‘s orbiter . Also it could prevent a extremely high G-Force peak just before MECO . But some MLVs like Atlas 551 and Delta II / Delta IV M does not follow this rule--they usually have a good liftoff TWR by using some small solid rocket boosters attached on the side to help the stage 1 to kick off from the surface with sufficient speed , despite the fact that solid rocket boosters’ Isp is lower than that of liquid fuel engines , it still improved efficiency since its gravity losses is lower than that of low TWR rockets . A more advanced solution is common core booster design , which is used on Delta IV heavy and Falcon heavy , using three parallel identical large liquid fuel boosters , and the center core throttle down to let it burn up after the two side boosters .
The second factor is delta-v . Despite the fact that delta-v is not net velocity change but it is directly related to your velocity change counting gravity loss , especially MECO velocity . MECO velocity determines the second stage’s lowest initial TWR . For example , if your MECO velocity is only around 2.7 km/s like SpaceX Falcon Heavy , the second stage TWR must be at least 0.9 , but if your MECO velocity is 4.3km/s like most real HLVs , you will be able to lower your second stage TWR to 0.36 . That’s because the larger the MECO velocity is , the less time the second stage will take to circularize its orbit , and thus the less gravity losses it will suffer from . From another aspect , the more horizontal velocity the 1st stage pick up , the more centrifugal force the second stage will get , the less gravity pull the second stage will suffer from . So that’s why despite having a mere 1.5km/s difference which is only 18% of the total delta-v consumption , there is a huge difference in the second stage’s initial TWR .
The third factor is Isp . This is not a major factor in ascent profile , but it affect ascent profile in a special way . That’s because , with same thrust , if you have a higher Isp , you will get a lower propellant flux , and the increase in TWR will be slower . For example , with a start TWR of 0 . 3 , and a same 6000 delta-v , let’s compare the mass change between a liquid hydrogen NTR(1200s Isp) stage and a UDMH-NTO ( 300s Isp ) chemical rocket . Referring to the rocket equation:delta-v=Isp*ln(mi/mf) in which mi&mf stand for initial and final mass , if they are both 500t and 0.3 TWR at beginning , and let’s make a rough estimation assuming Earth G is 10m/s2 , so the NTR stage’s final mass is 303.265t(=500/e^0.5) , and the LH2-LOx stage’s final mass is 67.67t(=500/e^2) . So the final TWR are 0.4946 and 2.216 , and mean TWR is 0.385 and 0.815 , it’s a very big difference . So if you are using D4H method which I will mention later , when launching exactly towards east , if you use a LH2-LOx upper stage with initial TWR 0.28 , your GTO orbit’s long axis will have a 60°angle with your launch point from the center of the Earth , but if you use a hydrogen NTR upper stage also with initial TWR 0.28 , the angle will become 90 degrees .
These theoretical factors mentioned above can be applied to a launch at any planet with atmosphere, like Mars and Venus landers. Now here I provide you some basic facts about an Earth orbital rockets. Firstly the delta-v requirements for a LEO launch is about 9000m/s for high TWR rockets , and about 9500m/s for low TWR rockets . And LEO height is also different, about 160km for high TWR rockets , and at least 300km for low TWR rockets or you won’t have enough time to circularize your orbit . Also , for a reasonable LEO launch , the first stage will need to boost the rocket to at least 3.5km/s to ease the burden on the second stage when fighting with gravity and winning circularization time . To achieve this , you need to have more than 4.5 km/s in the first stage ,and if your first stage SLT is lower than 1.25 , you may need to pack more than 4.8 km/s in the first stage since the gravity loss at beginning will be incredibly high . Make sure to remember all these basic data for a LEO ascent and then we will be able to move on to the analysis of my hypothetical rockets , since I will not mention these basics again , these data will be common sense since then.
I've built three hypothetical ships , and I'll take them as example . Actually , the first one is a typical LLV , the second one is a specially designed HLV which lacks real-life counterpart , and the third one is mainly for special needs to directly inject the vessel into a high energy orbit with a design quite a bit more radical than real Delta IV Heavy .
The first one is QueQiao LV , a typical light launch vehicle . It is designed to carry a 750kg-ish payload to TLI . It also has a seperate 3rd stage rocket motor to do the TLI burn some time after reaching LEO , so counting the mass of the TLI rocket motor , its LEO payload is about 2.1t and let's only focus on the LEO ascent part .
In this ship's design , due to the complete lack of 200kN-level surface-optimized engine existed in history , I used a vacuum engine (Russian RD-0124 , 1990s) which offers a good 359s Isp in vacuum but a mediocre 245s Isp at sea level (the 245s sea level Isp is much worse than surface-optimized ones which is approximately 302s but is much better than most vacuum engines which have less than 200s Isp at sea level which is too poor to use ). So I chose XiChang Launch Center which have a high altitude and increase Isp and SLT a lot , making it a lot efficient than launching from Cape Carnival at the same latitude , but a lot lower , thanks both to higher Isp(higher delta-v) and higher SLT(much lower gravity losses) .
In fact the TWR of this rocket is pretty high since the Isp and thrust increase a lot since altitude increase rapidly , as a result , the final acceleration of the boosters and center stage 1 is extremely high , both up to 7gs .
Also the second stage TWR is very high(0.8 is incredibly high except the Falcon Heavy carried out by SpaceX since the MECO velocity of that is way too low , only up to 3km/s surface) . That's because all the engines have a large thrust , and the Isp of S1.5400/RD-58 series is really quite high , up to an astonishing 361s for RD-58M-CCN built around year 2000 , relative to common kerosene-LOx engines which usually has a vacuum Isp of 340-345s for vacuum-optimized ones , and 336-338s for advanced surface-optimized ones .
So the trajectory turn out to be a continuously ascending curve which goes quite flat in the end at orbital insertion point . And here comes the ascent profile:For stage 1 , pitch your velocity vector to 82deg above horizon at 1200m/s , then follow prograde and pitch 1-2 degrees up or down to make the pitch relative to horizon 45deg at 700m/s , and 25deg at boosters separation , then focus on ascent rate which is 700m/s at boosters separation , pitch up a little when velocity vector drop below 10deg to horizon . This way you will control the MECO ascent rate precisely 460-470m/s . Then keep thrusting prograde until ascent rate drop below 20m/s at 6 . 2km/s surface . Then pitch up to about 3 degrees to keep vertical velocity precisely zero at all time . Then you will get into a 141-160km circular orbit with this for sure .
Fig.1 Telemetry data record of the ascention of QueQiao LV . (The orbit is a bit lower due to minor mistakes)
*The purple line indicate the ship’s angle of attack’s vertical part .
The next one , Moon Odyssey HLV , is a heavy advanced rocket to deliver a docking-free 5t Luna lander . (* Note that the Isp of Methane solid core NTR is unrealistic ; the real performance may be around 500s , which sounds not good news , since Methane has only 1/2.828 efficiency relative to LH2 but a afterburning LH2-LOx solid core NTR has a similar propellant density and Isp which can serve as a replacement . This is actually a mistake in simulation )
I used a half-hypothetical RO Raptor ( Surface Variant ) engine ( uses one of these information in Elon Musk’s meetings ) , and a methane NTR as the second stage .
Since the second stage ignition TWR is fairly low , and the 1st stage dv is not quite enough(2nd stage efficiency is way higher than 1st stage , since it has a much higher Isp , so increase its portion) . So S2 ascent is pretty hard to execute .
And another annoying thing is that the SLT of S1 is also quite poor , only 1.18-it's common in many HLVs such as Saturn V , with a extremely low 1.13 SLT , which sacrifice almost 88% of dv to gravity at the start of ascent , causing a great gravity loss when it is rising up slowly from the launch pad . However adding more fuel is actually , a lot cheaper than adding engines . So low TWR is mainly for economic reasons .
So the strategy here is to turn gently at start . The ascent profile for this rocket is as follows:I turn 3 degrees one by one at 40 , 70 , 130m/s , so that its surface velocity's prograde vector will pitch to 85 degrees at 100m/s . From then on , just keep it pitch 1 degree over prograde so that even when the turn became pretty quick at 200-500m/s due to lowered pitch over horizon , it will still be able to maintain its pitch 45 degrees relative to horizon at 1000m/s surface , which serves as an important checkpoint .
Then I'll have my MECO at 3 . 2km/s surface and have an apoapsis at 300km at 170km altitude . Thus the ship will have a very large vertical velocity , over 1 km/s , to help the low TWR stage 2 fight against gravity through comsuming vertical velocity and gain enough circularization time .
However , only using the vertical velocity of stage 1 is not enough . So the stage 2 still need to pitch up a lot to maintain altitude and prevent the ship from falling too fast and result in a fiery explosion due to severe overheat in atmosphere . Well I gained from experiments that 28 deg pitch over prograde is nearly perfect for a LEO insertion at about 310km , when the maximum reached altitude during ascent is 350km—The ship actually insert into LEO well after the time it reached its apoapsis . This is purely because the low TWR of stage 2:It will be impossible for a craft like this to enter LEO before apoapsis with such a small stage 1 dv and . Falling , at here is not important since you are , still well out of the atmosphere . (However it will be a minor issue for manned mission:if engines were disabled by accident and mission was forced to abort , the ship will go a sub-orbital reentry which have a extreme peak G-Force:the Soviet Soyoz 18a in real life which was aborted due to launch failure so it entered atmosphere at an apoapsis of 192km , and the peak G is an astonishing 23G which caused minor problems for astronauts;if apoapsis is 280km , as I tested during the recovery of the Raptor engine , the peak G-Force will be at over 40g for about 10 seconds , large enough to kill astronaut;fortunately most engines are very reliable at present)
(the data recorder exceeded its maximum recording time and I have to break the record into 2 parts)
Fig.2 Telemetry data of Moon Odyssey HLV( aod indicate the ship’s absolute angle of attack’s vertical part . )
Note aod have a few changes over time since I’m manually controlling it with the assistance of Smart A.S.S. and the aod I used(about 28deg) is an experimental value , not exact
A more radical approach is the D4H(Delta IV Heavy by ULA) ascent profile(for cargo mission only;for the same reason as mentioned above , I estimate that the peak deceleration G-Force after mission abort will be over 100gs , crushing poor astronaut(s) into pancake(s) and cause instant death) which aim to direct GTO injection without entering LEO . This method pitch up stage 1 severely , and at the meantime get the rocket a extremely high apoapsis and a very high rate of climb , and then the stage 2 will pitch less(about ~10deg over prograde) and burn a long time and at last directly insert into a highly elliptical orbit like Geostationary Transfer Orbit(GTO) or trans-lunar injection(TLI) . In this method it is impossible to inject into LEO but is can use a much smaller TWR of 2nd stage , as low as 0.28(it's almost fixed as this value come out of my experiment and 0.29 will get periapsis too high and 0.27 will crash into atmosphere and burn up resulting in catastrophic failure ). If you use an NTR , it will be very good , since NTR is very heavy and efficient , which means that 7500 m/s required in NTR ( Isp 622s ) is not too much , but it is a large amount in a chemical stage(Isp 320-460s) . So it maximizes the high efficiency of the nuclear stage by packing more delta-v on nuclear stage and the low TWR needed means it needs less nuclear engines so it has less dead weight , hence more efficient. As for historical launch vehicles , they don’t use nuclear engines , but they also use energetic LH2-LOx upper stage , which offers a excellent 460s Isp compared to 300-330s Isp foe most propellants . The major shortcoming is that launch time must be fine tuned since unlike departure from LEO which can let your long axis point everywhere you want , however in this ascent profile it is decided by launch time. So , moon departure window , is restricted from 2 per day to 2 per month . Also the engine must be very reliable ,suitable for long burns like RL-10 series or NTRs , so that they will not break down halfway during the ridiculously long orbit insertion burn .
Well the principle behind D4H ascent profile is relatively simple:when your speed is higher than the circular orbital speed at that height , centrifugal force will exceed gravity and the descending rate will decrease quickly . Thus high negative vertical velocity is not important;in fact the peak negative vertical velocity is about -1.2km/s , a lot higher than the method of pitching up to maintain altitude , in which the maximum descent rate cannot exceed 500m/s when initial TWR is 0.45 ( my experiment value ) , the lowest practical TWR for pitch-up method .
So I used a ship Lunacy( RF , not RO meaning these engines are still hypothetical despite having realistic-alike performance ) . In this simulation the profile is to let the prograde maintain a 30d pitch relative to horizon at MECO , and keep thrusting 10d pitched up relative to prograde . The total dv for the entire TLI ascent is 13.1km/s , a lot higher than 12.2km/s for common rockets , however less engines increase dv at the same mass , and less engine means lower total cost , which matches the ultimate aim of rocket design . The highest point in the curve is 850km .
So these are some parts of my LEO/GTO ascent profiles , and as I used a full kit of realistic mods , so the results is quite plausible , which may be applied to real-life launches with the same engines and similar fuel tanks . These computer simulations , can save much time while maintaining great accuracy . It also provide a way to learn rocketry without owning s SpaceX-alike company. So it can be used to instruct rocket design at the beginning when doing rough estimations .
I also want to imply that this method is reliable since all results are completely repeatable in any realistic simulation(especially KSP-RO where I develop these hypothetical rockets:without engine failures , the QueQiao LV has a success rate of over 80% and the Moon Odyssey has a success rate of over 50% with only manual control(no autopilot , but I used a smart pilot assist which requires manual control as numeric input))
Now we’ve sort out the basics of a LEO ascent trajectory design:at first we need to have 9.0-9.6 km/s of delta-v,then we will design its ascent profiles , based on the rocket’s stage TWR , delta-v distribution and Isp of its engines . Then fly it manually in simulation to optimize your trajectory and finally whtn your first stage can fly properly sending the vessel to a desired altitude and speed without much pitching from prograde then the gravity turn will be OK , and finally when you pitch your second stage at a certain angle and it enters a nearly perfect circular orbit around Earth at an altitude over 160km and your design will be successfully finished.
By:Kerbinator(My online name)
At Kerbin University of Aeronautics and Astronautics(KUAA)(Just for fun xD)
TFinal:20191101 7:54 a.m.
BASE:121 min on mobile
Overhaul:184 min on PC
Overhaul 2:114 min
Overhaul 3:62 min

后记
祝贺SLS成功发射。
本文作为教程,献给KSP+RSSRO的玩家们,以供作为参考使用。

