3.3 粒子探测器（二）

为了简化计算，我们将场假设为无质量标量场，可以得到正频Wightman函数为：

考虑探测器的轨迹为：

表示一个匀加速运动的探测器经过一系列复杂的计算可以得到跃迁振幅：

其中有一个Planck因子，表示探测器处于温度为：

热浴中。其实这就是著名的Unruh效应。

相同的效应可以在热场中发现。考虑一个探测器在热场中惯性运动，可以得到：

对比可以得到：对于一个加速运动的探测器，真空态是一个热态。

随后书中将真空态扩展为多粒子数态的情形得到Green函数为：

然后对于一个惯性运动的探测器它的响应函数为：

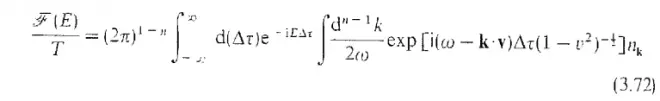
书中对这一段有详细的物理讲解，因为我们的重点不是这个所以不具体介绍。

一般来说，<N>与探测器测量到的粒子数之间没有简单的关系，即使粒子是自由下落的。然而，在一种特殊情况下，确实存在一种简单的关系。考虑一个在遥远的过去和未来都近似静止的时空，在与标准平面波模式相关的区域构建真空态，其形式为 (2.11)。这是通常的、物理的、无粒子的状态，在 "in "区域的惯性探测器肯定不会记录任何量子。

当然，如果时空只是渐近静态的，那么（3.55）中积分的上限严格来说就不再是无穷大了。我们假设单极子探测器的相互作用在探测器进入非静态时空之前被绝热关闭。同样，在非静态区域，探测器将在时空运动停止后绝热开启。如前所述，这种利用绝热切换将相互作用限制在有限持续时间内的假设在量子理论中很常见，只要相互作用的持续时间远远大于能量的变化（不确定性原理），切换过程本身对探测器的假激励就可以忽略不计。

在出射区，in模式一般不再是固定频率的平面波，如 (2.11)。那么，粒子探测器将如何处理出射区的in真空态呢？显然，如果量子场处于与出射区形式为（2.11）的模相关联的出射真空态，那么出射区的惯性探测器将不会记录量子。然而，正如我们将要看到的，如果量子场处于in真空态，探测器一般会记录到一些量子的存在、 为了找出探测器确实记录了什么，我们必须（结合（3.55））分析在出射区评估的怀特曼函数 G*（利用真空中构建）。这通常是位置变量 x、x'的复杂函数。我们可以利用Bogoliubov变换来简化计算的过程。最后的结果是：