【电路原理】分析换路后电抗元件的电压电流变化

在《电路原理》中涉及对动态电路的分析,其中就包含对电抗元件(电容、电感)的分析。本文在此分析8种不同的电路,借此以熟悉电抗元件之间的特性,8种不同电路的换路规律,以及对电路分析的方法及技巧。
以下为待分析的8种电路。

说明:
1、分析电压和电流时均采用关联参考方向,电抗上的参考方向已标出。
2、元件均为理想元件。
3、分析时单位采用国际SI单位制:电压(V、伏特)、电流(A、安培)、电阻(Ω、欧姆)、电容(F、法拉)、电感(H、亨利)。
4、开关S1、S2、S5、S6初始状态为开路,S3、S4、S7、S8初始状态为闭合。
5、本次分析,激励源均为直流。(其它激励波形也可仿照本文分析,但复杂很多。)
分析前所需了解并掌握的:
1.0、电容两端电压不能突变(具有阻碍电压突变性质),而电流可以。
1.1、通过电容的电流为i=C*du/dt,u为电容两端电压、C为电容容量。
2.0、通过电感电流不能突变(具有阻碍电流突变性质),而电压可以。
2.1、电感两端的电压为u=L*di/dt,i为通过电感的电流,L为电感自感系数。
3.0、电阻两端电压和通过电流关系为u=i*R,R为电阻阻值。(欧姆定律)
4.0、开关开路(断路)→强制电流为0,两端电压可为任意值。(R=∞,G=0)
5.0、开关闭合(短路)→强制电压为0,通过的电流为任意值。(R=0,G=∞)
6.0、理想电压源,强制两端电压为us。
6.1、理想电压源通过的电流为任意值,由外电路决定。
6.2、理想电压源内阻R=0。
6.3、理想电压源不可短路。
7.0、理想电流源,强制通过电流为is。
7.1、理想电流源两端的电压为任意值,由外电路决定。
7.2、理想电流源内阻R=∞。
7.3、理想电流源不可开路。
8.0、基本的电路分析知识。
9.0、微积分基础知识。
10.0、对于以下一阶线性非齐次微分方程,其通解为:[1]


电路分析:
求开关 开/闭 后,电抗元件两端电压和电流的变化(关于时间t的函数表达式)。
【I】——电压源,电容电阻,串联。

开关闭合前:
uc=U0;(U0为电容初始电压)
ic=0;
开关闭合后:
由KVL得:uR+uc-Us=0;(Us为电压源电压)
→R*i+uc=Us;
→R*C*duc/dt+uc=Us;

函数图像:

通过函数图像可以看出以下规律:
1.0、电容电压以负指数速度趋向Us。
1.1、电容电压是连续的。
1.2、经过3*RC时间,电压过渡95%;经过5*RC时间,电压过渡99%;经过7*RC时间,电压过渡99.9%。(函数图中RC=2)
1.3、经过5*RC后基本可认为电路完成过渡过程。
2.0、电容电流以负指数速度衰减至0。
2.1、在换路瞬间,电流跳变至最大值,电容可近似看做短路。
公式中各个参数对函数的影响:
1.0、U0决定电压曲线的起始位置。
1.1、U0影响电流曲线的起始位置(电流峰值)。(ic|t=0与Us差值呈正比)
2.0、Us决定电压曲线趋向位置。
2.1、Us影响电流曲线的起始位置(电流峰值)。(ic|t=0与U0差值呈正比)
3.0、R影响电压曲线趋向Us的速度(影响时间常数)。R越大,uc趋向Us越慢。
3.1、R影响电流曲线趋向0的速度(影响时间常数)。R越大,ic趋向0越慢。
3.2、R影响电流曲线初始位置(电流峰值)。(ic|t=0与1/R呈正比,R越大ic|t=0越小)
4.0、C影响电压曲线趋向Us的速度(影响时间常数)。C越大,uc趋向Us越慢。
4.1、C影响电流曲线趋向0的速度(影响时间常数)。C越大,ic趋向0越慢。
达到稳态:
uc=Us;
ic=0;
开关断开:
uc=Us;
ic=0;
【II】——电压源,电容电阻,并联。

开关闭合前:
uc=U0=0;
ic=0;
开关闭合后:
由于电阻R2和电压源并联,所以R2无法改变电压源的电压→不会影响电压源对电容的作用,可以忽略。因为电压源强制两端电压为Us,电容具有阻碍电压突变性质,即电压为U0,若Us≠U0,则电路无法分析。
若要使分析继续,必须在电容C2上串联一个电阻Rc(相当于电容内阻,图未画出),并令Rc→0。模型即转化为【I】型。利用【I】推出的公式,代入计算得:
当t=0(合上瞬间)
uc=U0=0,ic=∞;
经过极短的过渡时间后(<7*Rc*C,因为Rc→0,可认为过渡时间→0):
uc=Us,ic=0;
函数图像:

现实中的电路:
因为现实元件不是理想元件,会有各种寄生参数。在开关闭合时,导线电阻等会限制电流峰值,寄生电感也会在一定程度限制电流增速,所以ic并不会到∞A。对于低压小电容情况,电流还未升到很高时就已经完成过渡过程。对于高压大电容情况,电路中会瞬间通过非常大的冲击电流,有可能损坏器件。在电路设计中,这种情况是要避免的。
达到稳态:
uc=Us;
ic=0;
开关断开:
此时【II】模型可以近似为【I】型,电容初始电压U0=Us,向电压为0的电压源供电,R为R2。

函数图像:

【III】——电流源,电容电阻,串联

开关断开前:
uc=U0=0;
ic=0;
开关断开后:
由于电阻R3和电流源和电容串联,所以R3无法改变通过电容的电流,可以忽略。可知ic被电流源强制为Is。易知电容电压

函数图像:

通过函数图像可看出以下规律:
1.0、电容电压是线性变化的。
1.1、电容电压没有上限,会一直增加。
2.0、通过电容的电流一直是恒定值。
公式中各个参数对函数的影响:
1.0、Is决定电流曲线的值。
1.1、Is影响电压曲线的斜率(上升速率)。(斜率与Is成正比,Is越大斜率越大)
2.0、C影响电压曲线的斜率(上升速率)。(斜率与1/C成正比,C越大斜率越小)
在电路设计中,可以利用电流源给电容充电来获得线性变化的电压。如果电路没有改变,理论上电压会一直上升到∞,但现实往往有很多因素限制电压,比如电流源最大输出电压(非理想电流源)、电容耐压、空气(击穿)、开关、电路换路等。
达到稳态:
!没有稳态!
开关闭合:
闭合后电路与【II】模型开关断开后相同,可直接利用之前推出的公式。电容初始电压为U0(具体数值取决之前充的多少),Us=0。

函数图像:

注:在t=0时换路。
【IV】——电流源,电容电阻,并联

开关断路前:
uc=U0=0;
ic=0;
开关断路后:
由KCL得:ic+iR-Is=0;
→C*duc/dt+uc/R=Is;

函数图像:

通过函数图像可看出:
图像特性和【I】型几乎完全相同,具体可参考【I】型。
达到稳态:
uc=Is*R;
ic=0;
开关闭合:
因为电容有阻碍两端电压突变特性,而开关闭合短路了电容,即开关强制电容两端电压为0。此时情况参考【II】型、开关闭合。此时将会有极大的冲击电流通过开关。
当t=0时
uc=U0=Is*R,ic=∞;
经过极短的过渡时间后:
uc=Us,ic=0;
函数图像:

现实中的电路:
和之前一样解释,会有很多因素限制电流不会到∞A。然而巨大的冲击电流对电路是不利的,尽量需要避免。一般情况下,开关会承受大部分的,由电容释放出来的功率。因为现实开关不是理想开关,换路过程需要时间,此时电阻最大就在开关,会导致开关触点烧蚀等等。
【V】——电压源,电感电阻,串联

开关闭合前:
uL=0;
iL=I0=0;
开关闭合后:
由KVL得:uL+uR-Us=0;
→L*diL/dt+R*iL=Us;
→diL/dt+R/L*iL=Us/L;

函数图像:

通过函数图像可看出:
1.0、电感电压呈现负指数速度衰减到0。
1.1、换路瞬间,电感电压发生跳变为最大值。
2.0、电感电流呈现负指数速度趋向于Us/R。
2.1、电感电流连续。
2.2、经过3*L/R时间,电流过渡95%;经过5*L/R时间,电流过渡99%;经过7*L/R时间,电流过渡99.9%。(函数图中L/R=1)
2.3、经过5*L/R后基本可认为电路完成过渡过程。
达到稳态:
uL=0;
iL=Us/R;
开关断开:
因为电感具有阻碍电流突变的特性(维持电流=i0=Us/R),而开关断开即强制电流为0。两者相矛盾,无法分析。
若要分析继续,可以把开关想象成一个电阻,其阻值Rsw→∞Ω(符合断路性质)。列写KVL,得出式子,并令Rsw→∞,即得
当t=0时(开关断开瞬间)
uL=∞;
iL=Us/R;
经过极短的过渡时间后
uL=0;
iL=0;
函数图像:

现实中的电路:
因为现实中每个元件/物体/环境只有一定的耐压,过高的电压即刻可以击穿元件/物体/环境。比如空气:大约10kV高压能击穿1cm空气。所以电压并不会达到∞V。一般情况下这种击穿会发生在开关上。机械开关即击穿空气,半导体开关即击穿半导体导致开关报废。
这种电路在现实很常见。为了避免高压带来的危害,往往有很多的辅助电路去吸收高压。也有利用这种高压的,比如boost升压器,或者一个简易的电人装置hhhhhh。
【VI】——电压源,电感电阻,并联

开关闭合前:
uL=0;
iL=I0=0;
开关闭合后:
由于R6与电压源并联,所以R6无法影响电感L两端的电压,分析时可忽略。
可知uL被电压源强制为Us。可得电感电流

函数图像:
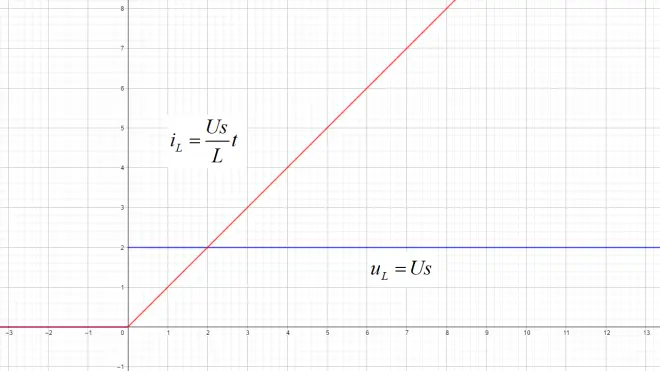
通过函数图像可看出以下规律:
1.0、电感电压一直是恒定值。
2.0、电感电流是线性变化的。
2.1、电感电流没有上限,会一直增加。
公式中各个参数对函数的影响:
1.0、Us决定电压曲线的值。
1.1、Us影响电流曲线的斜率(上升速率)。(斜率与Us成正比,Us越大斜率越大)
2.0、L影响电流曲线的斜率(上升速率)。(斜率与1/L成正比,L越大斜率越小)
在现实电路中,因为电感自身存在电阻,会限制其最大电流(与【V】型等同),电流并不会升到∞。还有一种情况是在达到最大电流前发生磁通饱和,此时电感将开始丧失电感特性,电流将不会再线性上升,而是突然爆升,最终受到电阻限制。一般会烧毁一些东西。
达到稳态:
!没有稳态!
开关断开:
此时I0为断开前的电流大小,Us为0。借助推导出的式子(见【VIII】型)得

函数图像:

注:在t=0时换路
【VII】——电流源,电感电阻,串联

开关断开前:
uL=0;
iL=I0=0;
开关断开后:
由于电阻R7与电流源串联,电阻R7无法改变通过电感的电流,分析时可以忽略。因为电流源强制流过的电流为Is,而电感有阻碍电流突变的特性(维持电流为I0)。若Is≠I0,电路无法分析。
若要使分析继续,需要假设开关S7为一个电阻,其阻值Rsw→∞Ω(符合开关断开性质)。电路可等效为【VIII】型(下文),代入其公式,可得。
当t=0(合上瞬间)
uL=∞,iL=I0=0;
经过极短的过渡时间后:
uL=0,iL=Is;
函数图像:

现实中电路:目前我还没有了解到这种设计,或者我孤陋寡闻了?
达到稳态:
uL=0;
iL=Is;
开关闭合:
闭合后电路可与【VI】开关断开时相似,I0=Is,Is=0,得

函数图像:

【VIII】——电流源,电感电阻,并联

开关断开前:
uL=0;
iL=I0;
开关断开后:
由KCL得:iR+iL-Is=0;
→uL/R+iL=Is;
→L/R*diL/dt+iL=Is

函数曲线:

通过函数图像可看出以下规律:
1.0、电感电流以负指数速度趋向Is。
1.1、电感电流是连续的。
1.2、经过3*L/R时间,电流过渡95%;经过5*L/R时间,电流过渡99%;经过7*L/R时间,电流过渡99.9%。(函数图中L/R=2)
1.3、经过5*L/R后基本可认为电路完成过渡过程。
2.0、电感电压以负指数速度衰减至0。
2.1、在换路瞬间,电感电压跳变至最大值,电感可近似看做断路。
公式中各个参数对函数的影响:
1.0、I0影响电压曲线的起始位置(电压峰值)。(uL|t=0与Is差值呈正比)
1.1、I0决定电流曲线的起始位置。
2.0、Is影响电压曲线的起始位置(电压峰值)。(uL|t=0与I0差值呈正比)
2.1、Is决定电流曲线趋向位置。
3.0、R影响电压曲线趋向0的速度(影响时间常数)。R越大,uL趋向0越快。
3.1、R影响电压曲线初始位置(电压峰值)。(uL|t=0与R呈正比,R越大uL|t=0越大)
3.2、R影响电流曲线趋向Is的速度(影响时间常数)。R越大,iL趋向Is越快。
4.0、L影响电压曲线趋向0的速度(影响时间常数)。L越大,uL趋向0越慢。
4.1、L影响电流曲线趋向Is的速度(影响时间常数)。L越大,iL趋向Is越慢。
达到稳态:
uL=0;
iL=Is;
开关闭合:
uL=0;
iL=Is;

总结:
至此8个电路分析完成,此处简要总结8个电路在开关换路前后,电抗元件的电压电流变化:

【I】
闭合:uc从U0负指数趋向Us;
ic从峰值负指数趋向0;
断开:uc不变;
ic=0;
【II】
闭合:uc从0骤升到Us;
ic瞬时冲击电流;
断开:uc从Us负指数趋向0;
ic从峰值负指数趋向0;
【III】
断开:uc从0线性增加;
ic=Is;
闭合:uc从峰值负指数趋向0;
ic从峰值负指数趋向0;
【IV】
断开:uc从0负指数趋向Is*R;
ic从Is负指数趋向0;
闭合:uc从IsR骤降到0;
ic瞬时冲击电流;

【V】
闭合:uL从Us负指数趋向0;
iL从0负指数趋向Us/R;
断开:uL瞬时高压尖峰;
iL从Us/R骤降到0;
【VI】
闭合:uL=Us;
iL=从0线性增加;
断开:uL从峰值负指数趋向0;
iL从峰值负指数趋向0;
【VII】
断开:uL瞬时高压尖峰;
iL从0骤升到Is;
闭合:uL从峰值负指数趋向0;
iL从Is负指数趋向0;
【VIII】
断开:uL从峰值负指数趋向0;
iL从I0负指数趋向Is;
闭合:uL=0;
iL不变;
经过比较之后也可以发现:
【I】和【VIII】对偶,【II】和【VII】对偶,【III】和【VI】对偶,【IV】和【V】对偶。相互对偶的电路具有相似的响应和相似的方程表达式。

本文到此完成对8个电路的分析,感谢能阅读完全文的观众,若本文有误之处,欢迎指正。
——by HD-nuke8800
附录:
[1]:摘自 同济版《高等数学》第七版 上册,第七章 第四节 一阶线性微分方程。


