【逻辑门的奇妙冒险】第6篇 见证第一个程序的诞生
本篇目标:
1.理解并实现寄存器间的加减运算;
2.理解并实现加载立即数到寄存器;
3.理解指令:形式化记录的操作序列;
4.实现指令的自动化执行,见证第一个程序的诞生;
5.算法初探:原地交换。
上一篇我们介绍了时序逻辑电路,拿到了通关奖杯,一个寄存器文件RegFile,上上篇的组合逻辑电路,也有通关奖杯,一个算术逻辑单元,ALU。这两个模块就是我们本篇要搞事情的重要器件,读者如果对这两个模块有什么疑问的话,建议回去阅读前两篇哦。
值得补充说明的是,由于Logisim这个小软件的能力有限,所有的模块都从与或非基础逻辑门开始搭建的话,运行起来会非常的卡。所以,我暂时把一些器件,例如加法器和寄存器,都用Logisim软件提供的现用模块来代替,原理都是那个原理,接口都是那个接口,除了让软件运行流畅一些之外,并没有区别。
为了让读者可以顺利地复现我的实验,复现我当初学习这种知识的“哇塞有意思哦”“这太美妙了”的体验,我接下来展示一下ALU和RegFile的内部实现和外部封装。首先是ALU的内部实现,异或、相等、大小比较等逻辑使用了已有的模块替换:

ALU外部的封装是这样的:

接下来是RegFile的内部实现,寄存器和大小比较用了已有的模块,0号寄存器还是常量0:

最后是RegFile的外部封装:

1.理解并实现寄存器间的加减运算;
首先,我们观察到,RegFile有俩输出,读数据嘛,ALU有两个输入,操作数嘛,看起来挺般配的,或许可以给它们牵个线?

我们将rdata1和A连接,rdata2和B连接,同时注意到wdata也是和Y也都是16比特,索性也连一块好了,这样一来,电路就是这样的:

简单思考一下,不难发现,wen和clk还是常量0,这种状态下的RegFile是不会发生变化的,我们可以把wen设置成1,clk接上真正的时钟。然后把RegFile和ALU看作一个整体,整理一下它们的输入:ALU的S,RegFile的waddr/raddr1/raddr2。电路变成这样的:

这个大电路现在有了四个输入了,只要指定一个输入组合,例如:
S=011,waddr=011,raddr1=001,raddr=010
就是把1号寄存器和2号寄存器的值进行加法,结果写回3号寄存器。
这里为什么是加法呢?因为ALU的选择信号S等于3的时候,Y等于A加B嘛。同样的,举一反三,如果输入组合是这样的:
(1)S=100,waddr=110,raddr1=100,raddr2=101
(2)S=010,waddr=111,raddr1=111,raddr2=110
(3)S=011,waddr=110,raddr1=110,raddr2=110
输入组合(1)的意思是把4号寄存器减去5号寄存器的结果写回6号寄存器;输入组合(2)的意思是把7号寄存器的值和6号寄存器的值作异或运算,然后写回7号寄存器;输入组合(3)的意思是把6号寄存器的值加上6号寄存器的值,写回6号寄存器。我们一般把raddr1和raddr2称作“源寄存器号”,把waddr称作“目的寄存器号”。通过输入组合(2)(3)我们可以知道,源寄存器号和目标寄存器之前没有限制,他们可以都相同的。现在,我们就可以实现任意两个寄存器间的运算,并且把结果写回任意一个寄存器了~
2.理解并实现加载立即数到寄存器;
对于第一步实现的目标,很明显还差点意思,硬件寄存器的初始值都是0,这些运算虽然都是对的,但是都是0显然太无趣了。我们能不能给寄存器加载进不一样的数呢?
我们注意到,现在RegFile的写数据wdata是连接到ALU的输出Y的,我们可以想办法让ALU输出非零的数。一个可能的方案就是,我们让0号寄存器加上一个我们想要的常数,再写回RegFile既可。现在的ALU两个输入是RegFile的两个输入,我们怎么上才能加上一个我们想要的常数,又不破坏第一部分搭建的结构呢?诶,我们可以用复用器,就像这样:
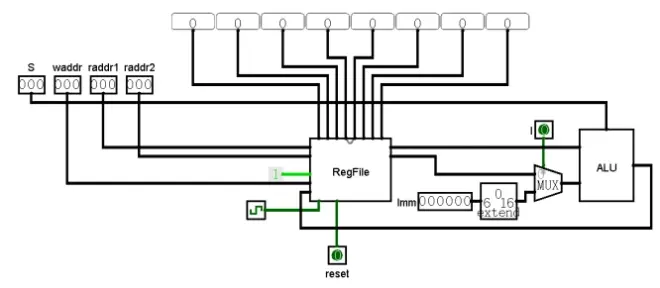
现在这个电路的输入多了两个,一个是否使用常数的选择信号imm和一个常数IMM(这个数有一个专用的名字,立即数,Immediate number,可以简写IMM,至于IMM为什么是6位再扩展到16位,这里留个坑,下篇解释)。现在我们可以试试新的输入组合:
(1)S=011,waddr=001,raddr1=000,raddr2=xxx,imm=1,IMM=32
(2)S=011,waddr=011,raddr1=000,raddr2=xxx,imm=1,IMM=48
xxx的意思是无所谓,反正也用不到,这样一来,我们的电路就会变成这样:

我们可以在RegFile拉出来的8个调试接口中看到,执行了输入组合(1)之后,1号寄存器成功地被写入32了,再来一个时钟,执行了输入组合(2)之后,3号寄存器成功地被写入了48了~
3.理解指令:形式化记录的操作组合;
我们刚刚上面两篇,已经有了两套输入组合的格式了,我们现在简单研究一下这些输入组合:我们一般先关注这次输入使用了ALU的哪一种运算?然后ALU是否使用立即数?目的寄存器号?第一个源寄存器号?第二个源寄存器号?立即数是多少?为了关注这几个问题,我们先调整一下电路输入,变成这样:

当我们回答了这些问号,也就是给出了一次输入组合,相应的,对电路的一次操作也就确定了。假如说我们想要按照一些顺序操作电路:
(1)1号寄存器写入31
(2)2号寄存器写入21
(3)3号寄存器等于1号加上2号
(4)4号寄存器等于1号减去2号
要完成这些操作,我们可以按顺序给电路这样的输入组合:
(1)S=011,waddr=001,raddr1=000,raddr2=xxx,imm=1,IMM=31
(2)S=011,waddr=010,raddr1=000,raddr2=xxx,imm=1,IMM=21
(3)S=011,waddr=011,raddr1=001,raddr2=010,imm=0,IMM=xxx
(4)S=100,waddr=100,raddr1=001,raddr2=010,imm=0,IMM=xxx
老是这么写也怪麻烦的,我们可以用一些符号来辅助记录,例如:
用“ADD”来表示S=011,且不使用立即数;
用“ADDI”来表示S=011,同时使用立即数;
用“SUB”来表示S=100
刚刚这些叫做操作类型,然后约定寄存器号用xi来表示,例如1号寄存器就是x1,2号就是x2,3号x3,以此类推。这些寄存器号按照waddr,raddr1,raddr2的顺序来写。如果是xxx无所谓的输入,我们就跳过不管,IMM就直接写。这样一来,我们的刚刚操作序列就可以这样写:
ADDI x1 x0 31
ADDI x2 x0 21
ADD x3 x1 x2
SUB x4 x1 x2
每一行都是一次形式化记录的操作组合,我们把它叫做“指令”。每一条指令都有它的二进制形式,也就是这些符号对应的二进制码,上面的这4条指令,二进制形式就是这样的:
011,1,001,000,011111
011,1,010,000,010101
011,0,011,001,010,000
100,0,100,001,010,000
后面两条指令为了对齐,补上3个零。这里就可以填个坑了,为什么IMM是6位的?因为这样一条指令正好16位。进一步地我们可以写出它们的十六进制码:
0x721f
0x7415
0x6650
0x8850
这种东西就叫做指令的机器码。显然机器是看不懂我们约定的符号的,那些是给人类看的,机器只认机器码的。
4.实现指令的自动化执行,见证第一个程序的诞生
现在我们知道了“指令”就是形式化记录下来的操作组合,一条指令就是要对我们的电路进行一次操作。这里我们可以约定,一次操作就占用一个时钟周期,下一个时钟周期我们就换一个操作。
显然,这些操作序列手动输入肯定得累死,我们应该让它们自动化地执行。如果有什么器件可以按顺序地给出这些指令作为电路的输入,应该就可以了。诶,我们之前玩计数器的时候,有一个器件可以做到,现在我们把指令的机器码接入复用器的输入

我们注意到,随着计数器的变化,指令按序选择出来,然后被分解成具体的输入组合。很自然地,如何我们把这个和完整电路对接起来会怎么样呢:

果然符合我们的预期,1号、2号、3号、4号寄存器按照我们的预期被写入正确的值了。自动化地执行一个指令序列,这就是一个程序,我们一起见证了在用与或非基础逻辑门搭建起来的电路中,运行了一个程序!而这个运行程序的电路,就是一个处理器!一个玩具型的CPU和它的第一个程序,诞生了!
5.算法初探:原地交换
现在我们有了指令,有了程序,然后就可以有算法了。但是我们现在的指令还比较少,暂时没法介绍复杂的算法。我们这里只是先暂时一个简单的操作:交换两个数的值。
比如说,我们用这样两条指令,给两个寄存器写入不同的值:
ADDI x1 x0 31 (011 1 001 000 011111)(0x721f)
ADDI x2 x0 21(011 1 010 000 010101)(0x7415)
现在我们要交换他们,使得1号得到21,2号得到31。很明显,不能将1号寄存器的值加上0写回2号寄存器,然后2号寄存器的值加上0写给1号。因为这个操作是有顺序的,一个时钟一条指令,第一次操作完成,2号寄存器的值就没有了。于是很自然地,我们就想到可以用第三个寄存器先暂时中转一下,指令就是:
ADD x3 x2 x0(011 0 011 010 000000)(0x6680)
ADD x2 x1 x0(011 0 010 001 000000)(0x6440)
ADD x1 x3 x0(011 0 001 011 000000)(0x62c0)
我们把这五条指令的十六进制码写出来,简单改造一下我们的复用器和计数器,试运行一下:

没有问题,符合我的预期,但是还是差点意思,毕竟这个算法污染了第三个寄存器,清理污染还得再多来一条指令。我们有没有什么办法让两个寄存器原地交换呢?可以不用到第三个寄存器?
这个还真的可以。我们需要先介绍一下异或运算(符号是“^”)的神奇性质:
如果A^B=C,那么C^B=A,C^A=B
这个性质读者可以自己证明一下,不难的。于是我们想到,利用这个性质,可以先让1号寄存器的值和2号寄存器的值做异或运算,结果写回1号;然后再让1号寄存器的值和2号的再异或一次,写到2号,此时2号的值就是1号的旧值了;最后让1号寄存器的值和2号再来一次异或,值写回1号,相当于1号和1号的旧值异或,得到2号的旧值。至此,完成了交换。乍听起来有点绕,直接看指令,然后结合上面的神奇性质,琢磨一下应该可以理解。
ADDI x1 x0 31 (011 1 001 000 011111)(0x721f)
ADDI x2 x0 21(011 1 010 000 010101)(0x7415)
XOR x1 x1 x2(010 0 001 001 010000)(0x4250)
XOR x2 x1 x2(010 0 010 001 010000)(0x4450)
XOR x1 x1 x2(010 0 001 001 010000)(0x4250)
直接上机看看效果:

很完美,直接原地完成交换,不需要借用第三方寄存器来中转。这其实就是更好的算法,用更漂亮的方式完成同样的目标。这一点将在后续两篇中有进一步探索~

