PLC和过程控制学习笔记2-数学模型的建立和拉式算法

几个重要概念：

静态模型：描述的方程和时间没有关系。用代数方程表示

静态关系：输出量与输出量之间的关系，用放大系数K表示

动态模型：描述的方程和时间有关系。微分方程或差分方程

动态关系：输出量y随着时间变化的关系，用时间函数T表示

连续时间和离散时间模型；

随机性：变量的关系是概率分布的；

确定行：能用函数关系表达的。

参数与非参数；

线性：可以用叠加原理；齐次性（均匀性）

叠加性如下:

可以满足叠加性的运算就有乘以常数、除以常数、积分、微分。

齐次性：

输入输出满足上述公式

非线性:(计算准则：通过泰勒展开保留第一个，其他的忽略)。

输入输出的过程描述：

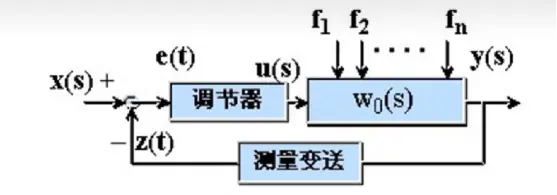
输入输出量的函数关系;

上面这个公式出现两个未知量，分别是被控量和扰动量的传递函数，要求传递函数现在就需要补充一点拉式变换的基础知识。

拉式变换

拉式变换的过程如下图所示：

通过拉式变换把时域的变为频域的方式（目的就是把微分项降次）化繁为简

拉式变换具体计算方法如下，我就直接贴图了：

下面就是拉式变换的一些性质了：

1. 线性

2. 位移性质，如下图：

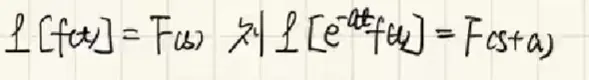
3. 延迟性质

拉式变换后尽量把等式右边整理成如下的形式：

比如

然后在计算的过程中有一个比较重要的微分定理如下：

在用到微分定理的时候会有一个比较重要的概念：零初始条件

现在拉式变换基本了解了，下面就是什么是传递函数：传递函数就是零初始条件下输出：输入的拉式变换，如下：