【最后十课】立体几何-重点全解!2023高考冲刺!第5讲

组合体的体积和面积
根据组合方式分为 补 割



几何体的 高 真的 很重要

之后一般会在作一条垂线,再利用勾股定理

旋转体其实更简单,基本都是研究轴截面
如



内切,内接问题
如,三棱锥内切球

立体几何常见方法

最短路径在高三不常考
当题目让求点到面的距离,或涉及它的时候,如果不想建系,考虑等体积法

扩大截面前可以先用脑袋思考一下大致截面长什么样子

发现用平行线法较为麻烦

改用延长线法,一般延长处于体表的线

将它一直延长到与其所处表面棱相交


之后确定具体点的位置

外接球问题
这里主要讲解通法,大多数时候都是可以用的,只是有时比较麻烦,这时就要考虑套模型
一般来说给的几何体会有一个面比较特殊
即圆心比较好找

再列一个方程找到关系

找圆心 作垂线 半径相等列方程,如下

立体几何第一问大题平行关系证明

平行问题核心 线面平行
线面平行三种思路

1.构造平行四边形

2.两个重要图形

3.造面面平行(这种方法一般步骤比较麻烦)
方法:过线端点作面的平行线

此题也可造平行四边形

还可用两个重要图形(这里也比较麻烦)

利用线面平行性质定理
当要证明线线平行时,一定要想到线面平行性质定理

大题第一问垂直关系证明
注意面面垂直性质定理及三垂线定理

垂直问题核心—线面垂直
逆推法很重要
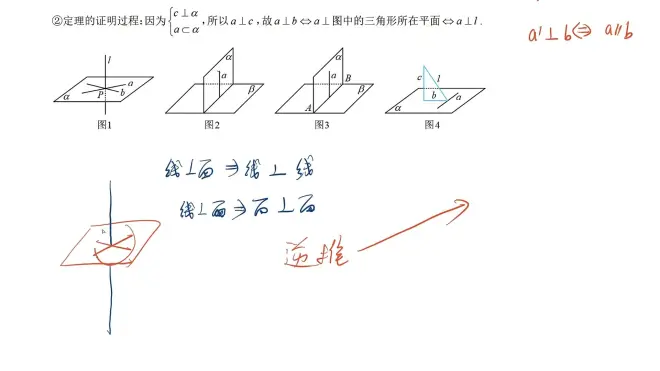
逆推典例

两种重要的隐藏在条件中的线线垂直
1.面面垂直性质定理得到
2.根据数据推得
当题目再复杂一些时

立体几何第二问
空间向量的计算
1.几何法

线线角:把两条线平移到一个三角形中(有时比用建系做简单)(如求异面直线所成的角)
线面角:一般直接作垂线,当不便作垂线时,可用等体积法求距离
二面角:有关二面角的条件,一定要翻译成平面角来做 (即线与线之间的夹角)
二面角两种做法
- 直接作射线
- 三垂线法

2.向量法(建系法)
投影向量——
判断向量共面方法——
基底——三个向量不共面即可

法向量运算:
1.平行与垂直问题


2.夹角问题
线线夹角:一定是锐角,余弦值一定是正的
线面夹角:一定是锐角,(看到面的问题,就想到转换为法向量问题)
面面夹角:一定是锐角
面面二面角:锐角或钝角
求正弦时---等于白给
求余弦时(正?负?)—①看图判断锐角钝角
当发现不好从图中判断时②尽量使一个法向量朝向二面角内部,另一个法向量朝向二面角外部(从而使法向量的余弦值与二面角的相等)

如图,此事不宜判断锐角还是钝角,已求得一个法向量指向外部,只需让另一个法向量z轴坐标为负即可使之指向内部

3.距离问题(步骤较为流程化)
点到直线(不常考)
点到面
9注意 当线面平行或面面平行时,直线到平面的距离,平行平面间的距离都可按点到平面的距离来算

一个常见的点的设法
动点设坐标

难点小梳理
动点问题
1.轨迹问题
轨迹为面
①

②

轨迹为直线
①

②

如 平行

垂直

轨迹为圆(题目较为死板)
但下面这种不常见

更多时候

2.翻折问题
注意1.不变的量(各种数据,如边长,角度)
2.与折痕垂直的量

如


