聊聊八卦~~~

Bootstrap可以说是唯一一个因为原理方法太简单而被Nature杂志拒稿的一篇文章。然而，现因其方法的朴素性、实用性被广泛应用于医学、金融和心理等领域。

进入正题

在医学研究中，我们常常通过单个样本的分布来假设、量化同一人群的分布，计算感兴趣的估计值，例如：均值、标准差和置信区间。然而，往往大多数统计学方法要求数据满足特定分布的假设，例如：样本服从正态分布。

然而，在真实世界研究中，这些假设可能不被满足。在这种情况下，有一种替代方法来估计标准误差和置信区间，而不依赖于假设的概率分布。

那就是Bootstrap，也有人称之为自助抽样、重采样技术。

Bootstrap原理介绍

这也可能是你唯一能听懂统计学方法。

Bootstrap方法最早由美国斯坦福大学统计学教授、美国统计协会总裁Efron在1979年提出的。其可理解为：对一个数据集中的观测值，采用有放回、且样本量不变的重复抽样，每个观测值每次被选中的机会都是相等的，因此有些观测值会被选中多次，而有些观测值根本不会被选中，新的抽样样本的观测数目与原始数据集相同，且同样代表了目标人群。其思想为：利用重复抽样的样本来进行总体推断。

常用于统计量标准误差的计算、未知参数的置信区间计算。

抽样后计算置信区间的几种方法示例：

举例：将一个容量为500的样本当做bootstrap总体，从中有放回的重复抽样，可以得到一个bootstrap样本，重复这个过程5000次，我们可以得到5000个bootstrap样本，通过5000个bootstrap样本我们可以得到5000个效应估计值（以中位数为例），那么我们如何计算这5000个中位数的95%置信区间呢？

1.Bootstrap正态近似法：计算5000个中位数的标准差，即为原始样本的中位数标准误差的估计值，如果抽样近似正态分布，则可以使用此构造中位数的置信区间。

2.Bootstrap百分位法：由于bootstrap样本分布是近似抽样分布，因此无需依赖正态性假设。相反，可以使用bootstrap样本分布的百分位数来估计置信区间。将5000个中位数按照数值从小到大排序，其中第2.5百分位数和第97.5百分位数就构成了一个置信度为95%的中位数置信区间。

3.偏差矫正的Bootstrap百分位法(bias-corrected bootstrap interval)：又叫偏差矫正和加速Bootstrap(accelerated bootstrap)。同样重复2的步骤，如果2构造的中位数恰好和原始样本的中位数相同，则选择Bootstrap百分位数法；若不相同，Edwards建议采用偏差矫正的Bootstrap百分位数法，其通过原始中位数在bootstrap样本中位数中的百分位点，矫正95%置信区间。

注意：Bootstrap法假设样本很好地代表总体，一般需要重采样5000次以上！

Bootstrap 方法实现
一、Bootstrap方法实现包括以下几个步骤：

（1）计算原始数据的感兴趣统计数据。

（2）从数据中对原始数据进行 B 次重新采样以形成 B 个bootstrap样本。重采样方式取决于要检验的原假设。

（3）计算每个bootstrap样本的统计信息。这将创建bootstrap分布，该分布近似于原假设下统计量的抽样分布。

（4）使用近似抽样分布获取bootstrap估计值，例如标准误差、置信区间以及支持或反对原假设的证据。

二、SAS案例：

数据是弗吉尼亚鸢尾花物种的50个随机选择的鸢尾花的萼片宽度的测量值。

data sample(keep=x);

   set Sashelp.Iris(where=(Species="Virginica") rename=(SepalWidth=x));

run;

 

/* 1. compute value of the statistic on original data: Skewness = 0.366 */

proc means data=sample nolabels Skew;  var x;  run;

 

%let NumSamples = 5000;       /* number of bootstrap resamples */

/* 2. Generate many bootstrap samples */

proc surveyselect data=sample NOPRINT seed=1

     out=BootSSFreq(rename=(Replicate=SampleID))

     method=urs              /* resample with replacement */

     samprate=1              /* each bootstrap sample has N observations */

     /* OUTHITS                 option to suppress the frequency var */

     reps=&NumSamples;       /* generate NumSamples bootstrap resamples */

run;

/* 3. Compute the statistic for each bootstrap sample */

proc means data=BootSSFreq noprint;

   by SampleID;

   freq NumberHits;

   var x;

   output out=OutStats skew=Skewness;  /* approx sampling distribution */

run;

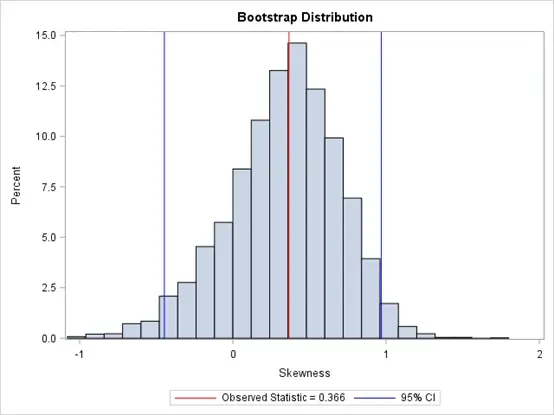
title "Bootstrap Distribution";

%let Est = 0.366;

proc sgplot data=OutStats;

   label Skewness= ;

   histogram Skewness;

   /* Optional: draw reference line at observed value and draw 95% CI */

   refline &Est / axis=x lineattrs=(color=red)

                  name="Est" legendlabel="Observed Statistic = &Est";

   refline -0.44737 0.96934  / axis=x lineattrs=(color=blue)

                  name="CI" legendlabel="95% CI";

   keylegend "Est" "CI";

run;

proc means data=OutStats nolabels N StdDev;

   var Skewness;

run;

/* 4. Use approx sampling distribution to make statistical inferences */

proc univariate data=OutStats noprint;

   var Skewness;

   output out=Pctl pctlpre =CI95_

          pctlpts =2.5  97.5       /* compute 95% bootstrap confidence interval */

          pctlname=Lower Upper;

run;

proc print data=Pctl noobs; run;

参考文献：

Efron B. Bootstrap methods: another look at the jackknife[M]//Breakthroughs in statistics: Methodology and distribution. New York, NY: Springer New York, 1992: 569-593.

如需Bootstrap详细资料PDF版本的小伙伴请后台联系！

关注微信公众号，获取更多相关内容！ 

编辑：天涯二毛君

审稿：老陈