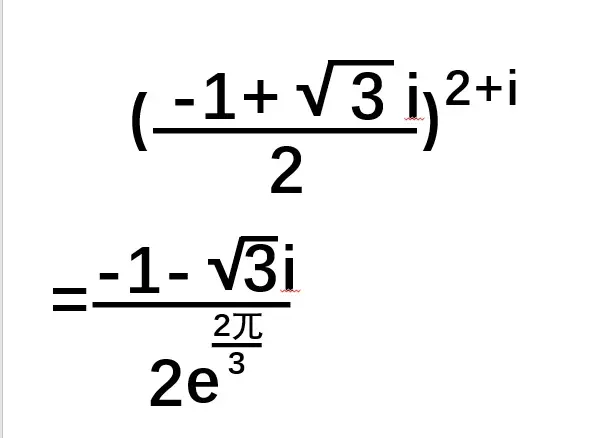复数指数幂运算（本文章只讨论主值）

对于任意2个复数：a+bi和c+di，像下图一样，如果a+bi是底数，c+di是指数，那就应该怎么算呢？结果又是什么呢？

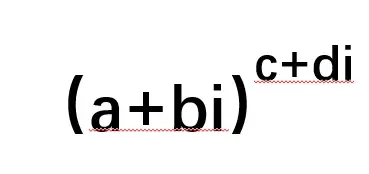
我们知道，对于任何复数，除了可以写成1个实数与1个虚数的和以外，还可以写成极坐标的形式。于是，原式就转化成下图了：

然后，我们就可以根据幂的运算，把括号展开，得到下面这个东西了：

似乎看到胜利的曙光了。可是，黑色的都很好算，标红的那个怎么算呢？

我们知道，对于任何数r都可以写成以e为底的形式：

这样一来，我们也可以将红色部分写成以e为底的形式，原式可转化为下图：

可以看到，分子上的e对应的指数有i,于是，可以根据欧拉公式，就能得到最终的指数没有i的结果了：

我觉得这已经足够了，当然你也可以把上图中黄框里的东西代入，并把sin和cos里的东西用和角公式展开，这里我就不进行这些操作了。

example：

要计算左边的式子，把右边的6个值代入我们得到的结果，就可以算得：