卷积码的 BCJR 译码算法 (二)--计算 γ

录制的视频：https://www.bilibili.com/video/BV1dx4y137zi/

前面文章已经推导出来下面这个状态转移的条件概率，这个概率是进一步计算发送比特后验概率的基础。

为了后面表达方便，我们把 (1)  中等号右边的三个部分，分别记为：

则公式 (1) 就可以简写为

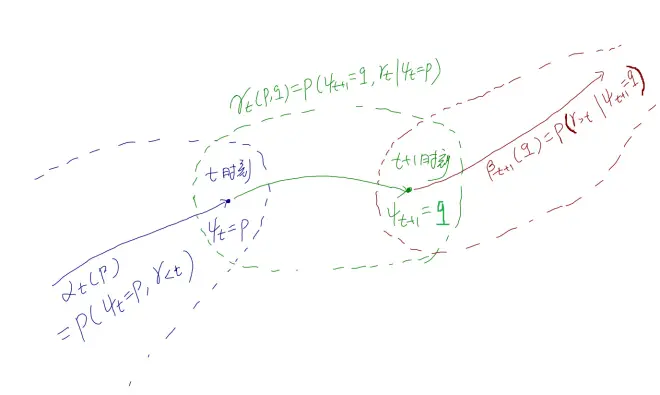
公式 (2) 中的 第二个，实际上是可以计算的，我们做一下推导：

其中

公式 (4) 的含义，就是在 t 时刻状态为 p 时， t+1 时刻转到状态 q 的概率，也就是在 t 时刻，输入的比特是让状态从 p 转到 q 的值，例如，在第 6 时刻，状态是 1，那么转到 第 7 时刻状态为 2 的概率，就是在 6 时刻输入比特是 0 的概率，因为输入 0 ，能让状态从 1 转到 2 .  一般是等概率的假定，所以，这个一般就是 1/2.

再来看公式 (3) 中的另外一块：

上面的含义，是从 t 时刻的状态 p 转到 t+1  时刻的状态 q 的条件下，收到是 r_t 的概率。"从 t 时刻的状态 p 转到 t+1  时刻的状态 q "  对应的是一个输入比特，我们记为 ， 此时，对应一个输出 ，经过调制后得到数据为 a .  数据 a 通过高斯高斯白噪声信道送出，多个数据依次通过信道送出:

各自都是符合均值为 0 方差为 的高斯分布：

多个数据，即卷积码一个比特输出产生多少个比特的输出，我们记为 Q 个，则公式 (5) 为：

我们举个例子说明一下，例如 t=6 ， 即时刻 6. 状态 从 1 转到 2，则我们计算的概率为：

其中：

把 (7) 代回 (6) 即可计算。我们在计算过程中，把公式 (6) 中的 1/2 和公式 (7) 中的 都忽略掉不参与计算，因为这些在计算过程中都是不变的，最后在计算概率归一化的时候，能把他们消除掉。