【菲赫金哥尔茨微积分学教程精读笔记Ep147】Bolzano-Cauchy第一定理证明（1）

80关于函数取零值的性质

a.定理

Bolzano-Cauchy第一定理：函数f(x)在闭区间[a,b]内定义且连续，又在这区间的两端点处取得异号的数值。则在a与b之间必能取出一点c，在这点处函数等于零。

即——

1. 函数f(x)在闭区间[a,b]内定义且连续；

2. f(a)f(b)<0；

3. ∃c∈[a,b]，f(c)=0。

b.几何含义

意义：连续曲线从x轴的一方转移到另一方，则它必与这轴相交。

c.证明

Bolzano方法（二分法）：

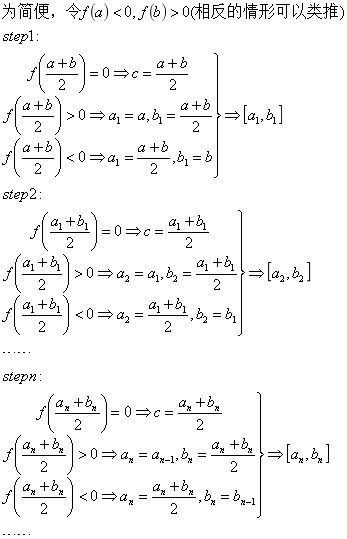
如果上述步骤无限进行下去——

——所以必然