高等教育自学考试(自考)离散数学(02324)视频教程

第一章 命题及命题公式



1. 命题与连接词
在数理逻辑中把能够判断真假的陈述句称为命题。
一般用小写英文字母或小写英文字母带下标表示命题。
命题包含两个要素:
- 陈述句
- 能判断真假
原子命题:不可再分解的命题。
复合命题:可以分解成多个原子命题的命题。
通常用符号来表示一个命题,这个过程称为命题的符号化。
常用的命题联结词:
- 否定联结词 --> 取反(¬)

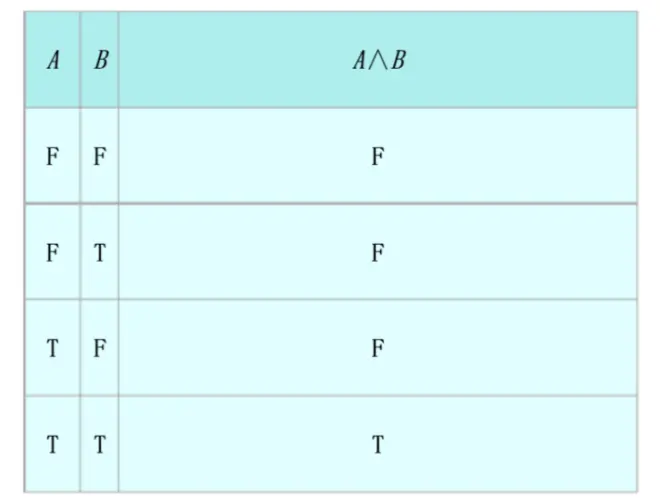
- 合取联结词 --> 与操作(∧)
- 析取联结词 --> 或操作(∨)

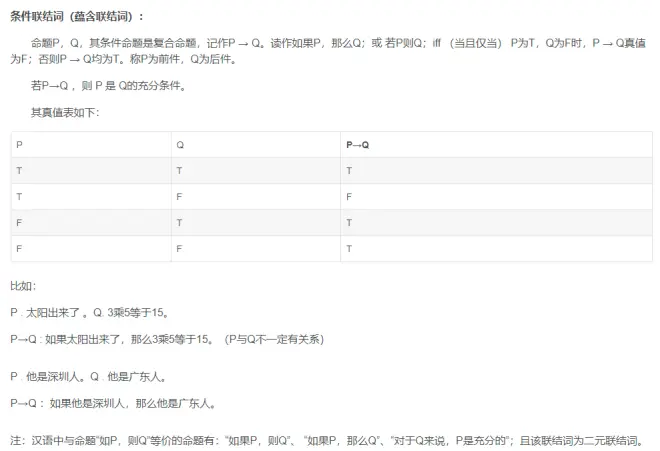
- 条件联结词 --> if (->)
- 双条件联结词 <-> 两个命题同时同样值是为真

2.命题公式的等值演算
按下列规则构成的符号串称为命题演算的合式公式,也称为命题公式,简称公式。
- 单个命题变元和常元是合式公式。
- 如果A是合式公式,那么¬A也是合式公式。
- 如果A和B是合适公式,那么(A∧B)(A∨B)(A->B) (A<->B)是合式公式。
- 当且仅当有限次地应用了1,2,3,所得到的符号串是合式公式
命题公式一般是用大写的英文字母A/B/C...表示。
规定联结词的优先级由高到低依次为:
¬ ∧ ∨ -> <->
命题公式中的命题变元,也称为命题公式的分量。
命题的符号化可按如下步骤进行:
- 找出符合命题中的原子命题。
- 用英文字母表示这些原子命题。
- 使用命题联结词将这些英文字母连接起来。
若指定的一种指派使A的值为真,则称这组值为A的成真指派。
若指定的一种指派使A的值为假,则称这组值为A的成假指派。
在命题公式A中,对A的每一个赋值,就确定了A的一个真值,把它们汇列成表,称该表为命题公式的 真值表。
设A和B是两个命题公式,设P1,P2,....Pn为所有出现于A和B中的原子变元,若给定P1,P2...Pn任一组真值指派,A和B的真值都相同,则称A和B是等值的或者等价的,记为A<=>B.
证明两个命题公式等价的方法:
方法1-----真值表法。
根据等价的定义,用真值表证明。
证明公式 p->q <=> ¬pVq

方法2-----等价演算法。
基本思想:先用真值表证明一组基本等价式,以它们为基础进行公式之间的演算。基本等价式常叫 命题定律。
下面是常用的命题定律:





重言式 and 矛盾式
设A是任一命题公式
- 若对A的任意赋值,其真值永为真,则称命题公式A为 重言式 或 永真式
- 若对A的任意赋值,其真值永为真,则称命题公式A为 矛盾式 或 永假式
- 若A不是矛盾式,则命题公式A为可满足式
- 由此定义可以看出,任何重言式都是可满足的。
蕴涵式
设A和B式命题公式,若A->B是重言式,则称A蕴涵B,记为A=>B.
证明蕴涵式的方法:
- 真值表法,即构造命题公式A->B的真值表。
- 等价演算法。
- 对A指定真值 T,若由此推出B的真值为T,则A->B是重言式,即A=>B(蕴涵式).
- 对B指定真值 F,若由此推出A的真值为T,则A->B是重言式,即A=>B(蕴涵式).




3.联结词完备集
- 两个变元总共有8种不同的取值,有2^4(16)个不同的命题公式。
- 三个个变元总共有16种不同的取值,有2^8个不等价的命题公式。
- 两个变元总共有2^n+1种不同的取值,有2^n个不等价的命题公式。


第二章 命题逻辑的推理理论
第三章 谓词逻辑

