盘点高中数学有价值的二级结论!别学没用的!【必修篇】

高中数学二级结论(必修)
二级结论是一把双刃剑,一定要合理使用才能发挥其最大价值

不等式篇
"基本"不等式:


三(n)元基本不等式:(必须学)
解决多项和或积为定值的最值问题
使用条件:
使用条件与基本不等式相同,就是三(n)项和/积为定值,有最大值。
题型情况:
一般情况求导可以解决所有求最值问题,但是基本不等式可以规避庞大的计算,十分好用!

柯西不等式:(可以学)


使用条件:
①调节不等式中的系数,调节后结合基本不等式求最值
题型情况:
偶尔能使用,尤其关于向量的计算

②当两个括号内的数相互乘积为常数,可以考虑柯西不等式

权方和不等式:(可以学)

使用条件:
解决分式不等式,分子或分母的常数和为常数
题型情况:
对于某些分式求最值会很简单

三角换元:(可以学)
使用条件:两个平方和为定值,使用三角换元即可快速消元,减少未知数

题型情况:

函数篇
性质
奇偶函数

“四则运算“可借助奇函数为-,偶函数为+判断
常见奇函数形式:

奇偶函数是题目隐藏的做题条件,一般情况下对做题有着至关重要的作用


其他性质:(全部要掌握!!)

常见转化,高考会考,一定要数形结合!

基本初等函数
题型→比大小

泰勒展开:(随便)

使用条件:
特殊函数求值,其中x取很小的值(绝对值小于1),误差会相对较小
题型情况:
一旦使用,很方便


放缩式:(随便)

糖水不等式→越放塘,水越甜

使用条件:将两个不相等的数经过放缩变成相等

题型情况:分式比大小,一般,两个分式的分子与分母会有对应关系,而且是对数问题
对数结论

三角篇
奇变偶不变,符号看象限
和差化积,积化和差(随便)

实用,但在学有余力情况下可以多记记

万能公式:(随便)
可以将名统一,与函数保持一致

向量
向量的中线公式→
使用条件:三点共线外有一点,一个向量可以被另外两个表示出来

等比分点

等和线(随便)

题型情况:系数和取值范围,题目少
向量的数量积
投影:(可以学)

极化恒等式:(可以学)

公式变形:(随便)


向量与三角形的四心问题(混个眼熟)

奔驰定理(随便)

无敌的直角坐标系!向量不会就建系
定点分比公式的向量表示与坐标表示(随便)

解三角形篇

几何结论
射影定理(可以学)
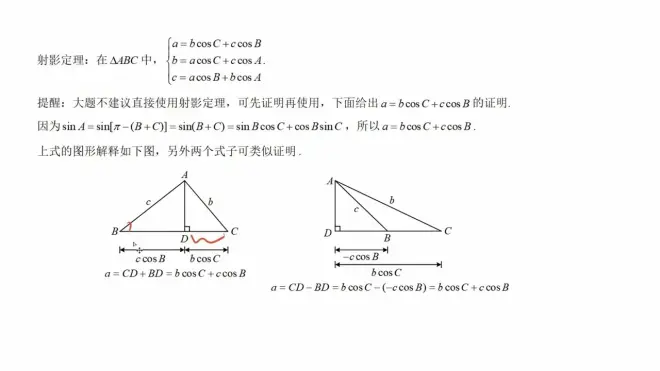
只要出现这种形式,直接带入射影定理就会直接得值。

双余弦法(必须学)

角平分线(必须学)

代数结论

随便

偶尔出现

立体几何篇

三垂线定理及其逆定理(可以学)

主要处理异面直线的垂直问题
异面→共面

外接球虽然很抽象,但是一般都会有着对应的模型,直接带入公式便可求出球的半径,进而解决各种问题

小结:东西太多啦!但是也一定要选着记呀!二级结论对于我们做大题还是小题在一定程度上都会有所帮助,但是,记就要记准确呀,千万别记错了!加油!(内容之后自己也会补充的,总之,希望对你有所帮助)

