高中数学：向量、余弦定理的数学建模与数学探究及应用

高一数学下册中6.4.3节学习了余弦定理和正弦定理，并通过向量法进行了定理证明。同步目标练习提供了如下一道关于数学建模与数学探究的理论实践结合的习题，值得讨论。题目如下：

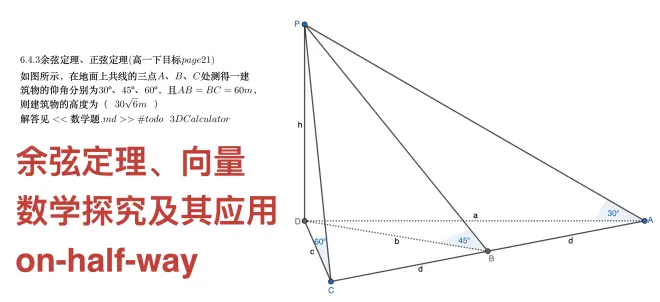
如图1所示，在地面上共线的三点 A、B、C 处测得一建筑物的仰角分别为30º、45º、60º，且 AB=BC=60 m，则建筑物的高度为（        ）

本题的解题分析思路及方法是和孩子共同学习过程中总结的，在我的如下视频中进行了详细描述，视频中主要记录了分析思路及主要方法步骤，计算过程不作为重点可自行完成。

视频讲解中提到的三种解题思路和方法总结如下：

首先，所给已知条件下无法直接计算出物体高度情况下，根据线面垂直知识及已知条件，可将所求高度这个未知数转化到其它边中，这样达到将所有已知条件和未知数集中到局部图形中达到求解目的。

方法一：依据余弦定理建立联立方程，约掉具有等长夹角边且互为补角的余弦项，得到三角形中线长公式，进而通过规避计算具体余弦角的方法通过所学余弦定理知识达到求解物体高度的目的。

方法二：通过高一数学第6章的向量知识进行求解，主要应用了向量的三角形法则和平行四边形法则，殊途同归得到方法一中获得的重要中间结论：三角形中线长公式。如同课本中通过向量法证明余弦定理一样，这里同样体现了向量的魅力。

方法三：既然本节主要讨论了余弦定理、正弦定理，那么能否通过这个更直接的公式进行求解呢？即如何得到角的余弦值成为解题关键。透过方法一互补角余弦互为相反数的知识的利用得到启发，如果能够求出互补角余弦值，也就获得了关键缺失条件，问题也就得到解决。本方法中利用了初中常用到的倍长中线知识构建了平行四边形，获得了三边已知比例的三角形，进而通过余弦定理推论求得对应补角余弦值，至此，解题的关键条件已经全部具备，余弦定理得到了完整应用。

如果你在学习中发现更多方法，欢迎留言补充！