《虚数不虚》第十二节 多值之问

上次，笔者带大家用计算机上制作了一张从f(z)=z到f(z)=z²的渐变动画。相信你已经有了一个初步感知。今天我们从一些基本图形入手，去进一步研究它的性质。

我们知道，如果我们把z写成极坐标形式r∠θ，那么f(z)=z²=(r)²∠2θ。为了验证模长平方，幅角翻倍的性质，我们首先选择三条条过原点的直线，以及一个圆心在原点的圆。

我们规定这幅图的X，Y轴，分别是朝下、朝右。因此，蓝、黄、绿、紫分别是第一、二、三、四象限，希望读者注意。

作变换：

f(z)=0.03*z^(1 + frame/30)

其中：

0.03代表把图像缩小原来的0.03倍

frame=1,2,3...30 （共30帧）

可以看到，两者在变换后保留了原来的形状，我们注意到：原来四个象限在变换后有两个象限合并到一起。我们从这种“二对一”变换得到启发，去研究复变换的另一个重要性质：多值性。

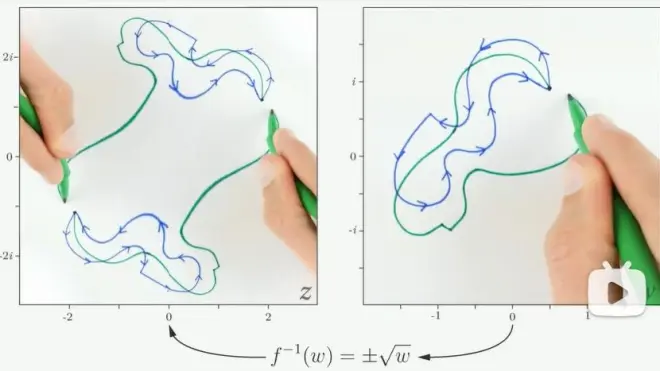
我们今天的主角是f(z)=z²的逆函数f(z)=±√z。这是一个“一对二”变换。

我们先来看一下正数部分f(z)=√z的变换：

作变换：

f(z)=5*z^(1 - frame/60)

其中：

5代表把图像放大5倍

frame=1,2,3...30 （共30帧）

随着幂逐渐减小，我们可以看到图像在逐步缩小变形，同时以X负半轴（黄、绿交界）为界不断向两侧拉展，最终形成了半朵“花瓣”。我们再把负数部分加进来，就得到了完整的“花瓣”。

作变换：

f(z)=5*z^(1 - frame/60)

及

f(z)=-5*z^(1 - frame/60)

frame=1,2,3...30

通过这个变换，我们多“复制”了一份空间。数学家把每一个空间称作“分支”(Branch)。为了研究各个分支之间的结构，最简单的方法是画一条闭合曲线。

在继续阅读前，读者不妨思考一下：我们会得到几条闭合曲线？

我们得到了两条闭合曲线。这符合我们的预期。但是，如果稍微改变一下，就会发生神奇的事情。

我们只得到了一条闭合曲线！

更进一步的观察表明，变换得到的两条曲线各跨越了一个分支，合二为一。

One reason I like math is that,  for many problems, someone much smarter than me has already given them some serious thought , and quite often found an elegant solution

Stephen Welch

正如这个视频的作者所言：数学的魅力在于领略先辈对问题透彻的理解。

下一节，我们将请出波恩哈德·黎曼，给我们回答这个问题。