郑涛（Tao Steven Zheng）著

【问题】

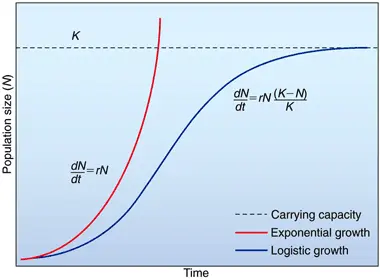
逻辑斯蒂增长模型（Logistic growth model）的微分方程是

其中 是种群增长速率（单位时间数量的改变）， 是比增长率 （proportional growth rate）， 是种群的大小（个体的数量）， 是可能出现的最大种群数承载力（carrying capacity）。

题一：求此微分方程的稳态解（steady-state solutions）？
题二：如果初始条件 ，求解微分方程。

【题解】

题一

稳态解（steady-state solutions）出现在 。 那么，

所以这个微分方程有两个稳态解： 和 。

题二

把微分方程 改写成 。

使用部分积分法（integration by parts）：

其中

因此，

令 ，所以

解初始条件问题：

因此，