（合计244字，用时30min——）

第四章 随机变量的数字特征

& 1 数学期望

定义：设离散型随机变量X的分布律为

若级数

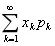
——绝对收敛，则称上述级数的和为随机变量X的数学期望，记为E(X)。即

设连续性变量X的概率密度为f(x)，若积分

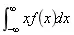
——绝对收敛，则称上述积分的值为随机变量X的数学期望，记为E(X)。即

——数学期望简称期望，又称为均值。

定理：设Y是随机变量X的函数：Y=g(X)（g是连续函数）

（i）如果X是离散型随机变量，它的分布律为

若级数

——绝对收敛，则有

（ii）如果X是连续型随机变量，它的概率密度为f(x)，若

——绝对收敛，则有

性质：