某倒角命题与衍生结论

几天前，同学发给我一道题，我对原题进行证明并挖掘了一些在此构型下的结论。

先看原题：

注意到ABHY共圆之后此题就不难了，下面给出证明：

此构型非常有意思，但本命题难度低下，我于是对此构型进行挖掘，得到了一些新命题：

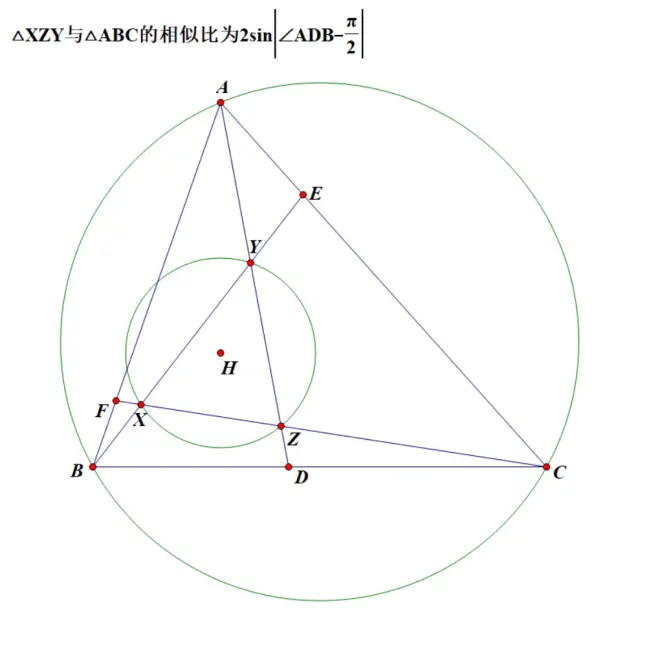
实际上，这里的Hagge圆完全是用来吓人的，我们将在证明中体现这一点

首先给出Hagge圆的判定：

先来看第一个结论：

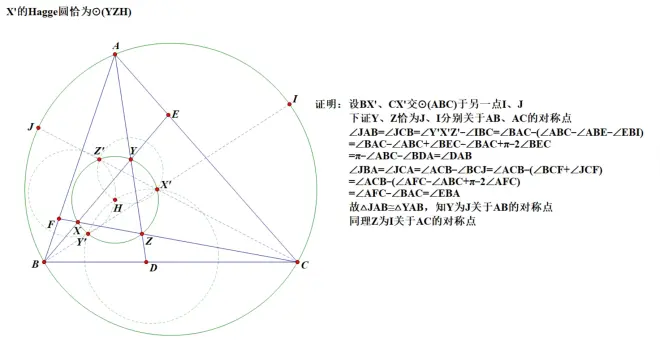
由Hagge圆的定义，不难看出X'实际为AD与△ABC外接圆第二交点关于BC的对称点，Y'、Z'以同样方式定义。那么，命题就得到了转化。

我们继续挖掘，在乱画的过程中发现：AY'Z'、BX'Y'、CX'Z'分别共线。不妨先承认此命题成立，那么，可以发现X'、Y'、Z'与X、Y、Z的定义方式相似，是使得∠(BC,Y'Z')=∠(AC,X'Y')=∠(AB,X'Z')的三条直线所交得的三个交点，并且∠(BC,Y'Z')=∠ADB，这样，命题又进一步转化，只需下面的引理即可得证：

而先前直接承认的命题可以通过简单倒角证明，于是原题得到了证明，下面给出解答：

由刚才分析中得到的X'、Y'、Z'的定义方式，可以仿照原题证明得到结论二的证明：

第三个结论，简单倒角即可：

在结论一已经证明的前提下，容易得到结论四的纯几何含量较高的证法：

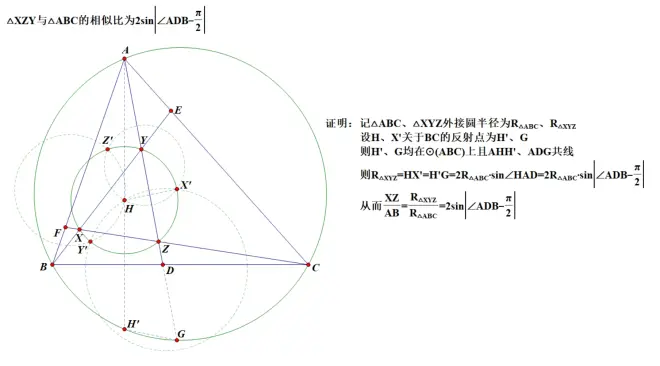
至此，所有命题得证

此构型应该还有一些未曾发掘的结论，不妨交给读者研究（虽然没什么读者qwq）