今天咱们来介绍一下零点差问题的解决方法。先从最基础的一类开始说起。

你看到这题的第一反应是不是极值点偏移？因为它出现了零点和关于零点的不等式。事实上，你确实可以称它为类极值点偏移问题，但这不会对你有任何帮助。

你最好叫这类题为零点差问题，因为这样你就记住了这类题的一个典型特征——零点的差。一般地，y=f(x)与直线y=m交于x1，x2两点，要求证x1-x2的绝对值大于或小于某个含m的式子的题就属于零点差问题。

三个关键点，

1.零点差的绝对值

2.含m的式子

3.直线y=m的交点

零点差问题我们介绍三种一般的解法。

1.切线夹

2.割线夹

3.曲线夹

切线夹适用于证明零点差小于某数的情况。

割线夹则在证明零点差大于某数时使用。

曲线夹在待证式出现根号时使用。

除此之外，零点差问题属于双变量问题我们之前介绍的方法仍然有可能适用。

第一期咱们先讲最基础的切线夹。

1.切线夹是什么？

切线夹就是用切线夹曲线。

切线夹是在解决这种

单峰函数与y=m形成零点的零点差小于某数时使用的方法。它的基本思路就是用函数上的两条切线夹住曲线。就像这样

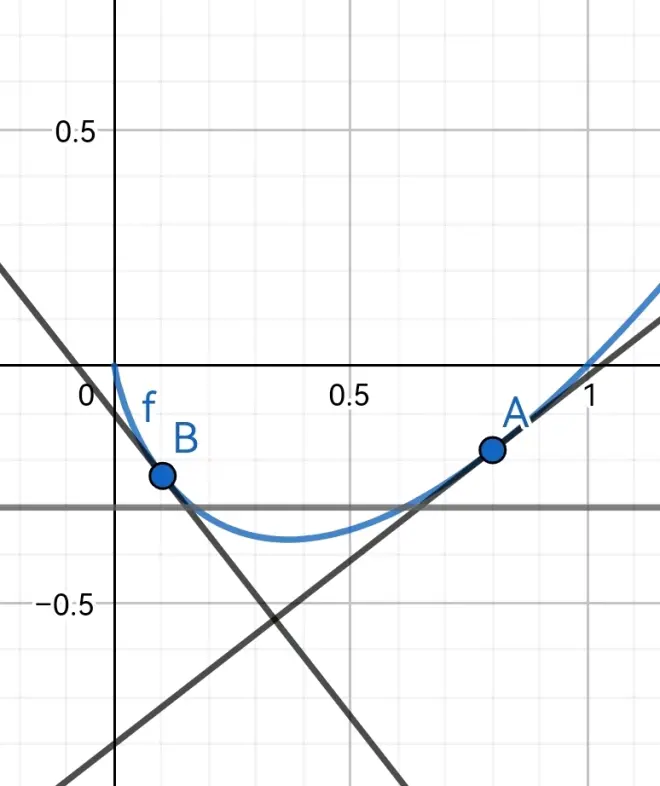
这时切线的零点差就大于等于割线的零点差。

所以切线夹的难点就在于找切线。

2.怪数突破

切线的寻找就必须要借助怪数了。

像是某个数的某次方，对数值，指数值这些数平常很少出现且他们一旦出现很难消除就是我们要找的怪数。

在这道题中出现里怪数e的-3次方，因此我们要找的切线很有可能就是函数在e的-3次方的切线。

3.系数搭桥

找到了第一条切线后就要想办法找第二条了。

题目右边是切线的零点差，而我们已经找到了第一条切线的零点，所以我们可以用对比系数的方法找到第二条切线的零点进而锁定第二条切线。

4.实战总结

刚刚那两条是最基本的想法，但根据我实战的经验。。。。。

大部分题你靠这种方法都能轻松找到切点。但少部分题。。。或许还是有困难。

这时可以用麻烦点的方法。

设切点，求切线，令y=m解出零点，再根据怪系数或怪常数这些怪数得到第一条切线。

第二条切线也可以再走一遍这个流程。

这种方法比一开始看到e的-3次方直接猜切点横坐标的e的-3次方要准。

5.题干信息

可是，这样你还是很难找到切线。这时请回头看第一问。零点差问题的第一问往往就是叫你求切线，这条切线往往就是你要找的第一条切线。(出题人也怕你做不出来)这时我们直接用系数找第二条切线就行。

比如这题

在真实的题目中会这样出

第一问求的恰好就是第一条切线。

6.常见值猜测

如果这些都失效了，你就猜一些常见的数。如0，±1，±2，±e，正负1/e，函数的零点处这样的切线。这是最后的不是办法的办法了。

7.答案书写

刚刚说了挺多大道理，可你该在答卷上留下什么呢？

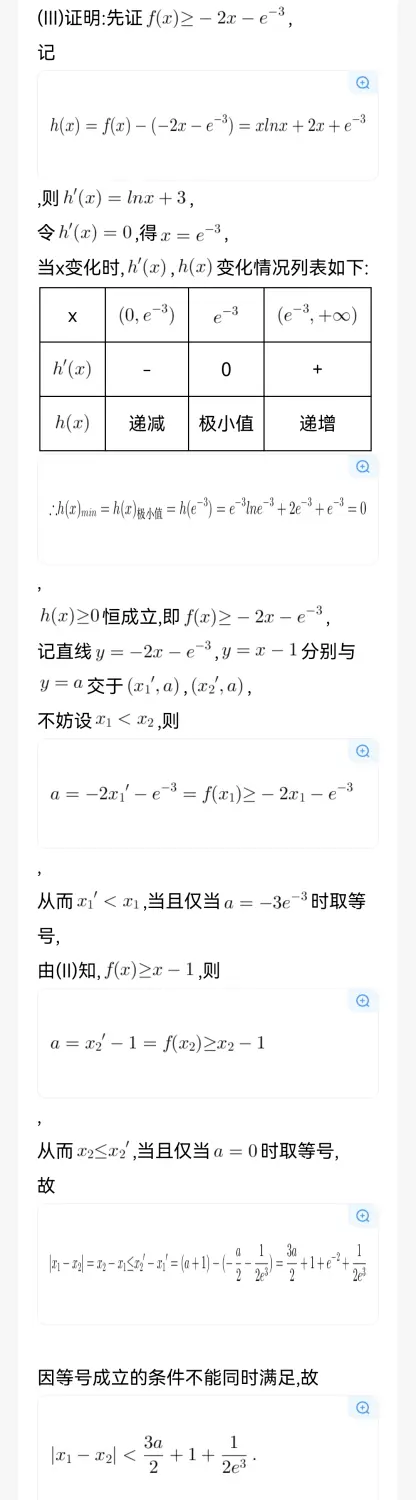
你就完全按照这个写，最好能在旁边配上切线夹曲线的图。这样就非常清晰了。

(前面的用构造差函数的方法证明切线和曲线的位置关系不能丢)