🔸学习量子计算、密码学、Space等Web3前沿技术

🔸认领Bounty，赚取赏金

🔸参与Hackathon，获得资助

更多Web3精彩技术分享尽在Dōjō👇

WeChat: @HackerDojo0

表示量子比特状态

您现在对比特以及我们熟悉的数字计算机的工作原理有所了解。现代软件中使用的所有复杂变量、对象和数据结构基本上都只是一大堆比特。我们这些从事量子计算工作的人称这些为 经典变量。使用它们的计算机，就像您用来阅读本文的计算机一样，我们称之为经典计算机。

在量子计算机中，我们的基本变量是量子比特：比特的量子变体。这些与普通位具有完全相同的限制：它们只能存储单个二进制信息，并且只能为我们提供 0或1的输出。然而，它们也可以用只有量子力学才能描述的方式来操纵。这为我们提供了新的玩法，使我们能够找到设计算法的新方法。

为了完全理解这些新门，我们首先需要了解如何写下量子比特状态。为此，我们将使用数学中的向量、矩阵和复数。虽然我们将逐步介绍这些概念，但最好是你已经熟悉它们。如果您需要更深入的解释或复习，可以在此处找到指南。(https://qiskit.org/textbook/ch-appendix/linear_algebra.html)

1.经典比特与量子比特

1.1 状态向量

在量子物理学中，我们使用状态向量来描述系统的状态。假设我们想描述汽车在轨道上的位置，这是一个经典的系统，所以我们可以使用一个数字$x$:

$$

x=4
$$

或者，我们可以将一组数放在一个称为状态向量的向量中。状态向量中的每个元素都包含在某个确定的地方找到汽车的概率：

$$
|x\rangle = \begin{bmatrix} 0\ \vdots \ 0 \ 1 \ 0 \ \vdots \ 0 \end{bmatrix}
\begin{matrix} \ \ \ \leftarrow \ \ \ \ \end{matrix}
\begin{matrix} \ \ \text{Probability of} \ \text{car being at} \ \text{position 4} \ \ \ \end{matrix}

$$

这不仅仅限制于位置，我们也可以设状态向量为汽车所有可能拥有的速度，以及所有汽车可能拥有的颜色。在经典系统中（像是上面所描述的汽车），当我们只需要一个数字的时候，使用这样一个巨大的向量是一件愚蠢的事。但是在本章节中，状态向量是一种很好的方式来存储量子系统的轨迹，包括量子计算机。

1.2量子符号

经典比特总是有一个完全定义的状态：在计算中的每一点，它们要么是0，要么就是1。对于经典比特没有比这更详细的信息了。因此，要写下经典比特（c）的状态，我们可以使用这两个二进制值。例如：

c = 0

对于量子比特，这一限制被解除。我们从量子比特中得到的是0还是1，只需要在进行测量以提取输出时确定。在这一点上，它必须承诺这两个选项之一。在其他任何时候，它的状态都比简单的二进制值更复杂。

要了解如何描述这些，我们可以首先关注两个最简单的情况。正如我们在上一节中看到的，可以准备一个量子比特，使其在测量时肯定会给出结果0的状态。

我们需要为这个状态命名。让我们缺乏想象力并称之为$0$.同样，存在一个量子比特状态，该状态肯定会输出1 .我们称之为$1$。这两种状态是完全相互排斥的。要么量子比特肯定输出0 ，要么肯定输出1 。没有重叠。用数学表示这一点的一种方法是使用两个正交向量。

$$
|0\rangle = \begin{bmatrix} 1 \ 0 \end{bmatrix} , , , , |1\rangle =\begin{bmatrix} 0 \ 1 \end{bmatrix}.

$$

这里由大量符号需要解释。首先，让我们解开这些奇怪的东西 |和 ⟩ 。它们的工作本质上只是提醒我们，我们讨论的向量表示标记为$0$和$1$的量子比特状态。这有助于我们将它们与比特值0和1或数字0和1区分开来。它是狄拉克符号法一部分，由狄拉克引入。

如果你不熟悉向量，你基本上可以把它们看作是我们使用某些规则操纵的数字列表。如果您熟悉高中物理课上的向量，您就会知道这些规则使向量非常适合描述具有量级和方向的量。例如，物体的速度用矢量完美地描述。然而，我们使用量子态向量的方式与此略有不同，所以不要太坚持你以前的直觉。是时候做一些新的事情了。

使用向量，我们可以描述更复杂的状态，而不仅仅是$|0 ⟩$和$|1⟩$.例如，考虑向量

$$
|q_0\rangle = \begin{bmatrix} \tfrac{1}{\sqrt{2}} \ \tfrac{i}{\sqrt{2}} \end{bmatrix} .
$$

为了理解这种状态的含义，我们需要使用数学规则来操作向量。具体来说，我们需要了解如何将向量相加以及如何将它们乘以标量。

提醒:矩阵加法和标量乘法(点击这里扩展)提醒:正交基(点击这里扩展)状态$|0⟩$和$|1⟩$组成正交基，我们可以表示具有这两种状态组合的任何 2D 向量。这允许我们用另一种形式来写量子比特的状态:

$$
|q_0\rangle = \tfrac{1}{\sqrt{2}}|0\rangle + \tfrac{i}{\sqrt{2}}|1\rangle

$$

这个向量，$|q_0\rangle$被称为量子比特的状态向量，它告诉我们关于这个量子比特的一切。目前，我们只能对这个状态向量的特定示例得出一些简单的结论：它并不完全是$|0⟩$且不是完全$|1⟩$。相反，它由两者的线性组合描述。在量子力学中，我们通常使用“叠加”一词来描述这样的线性组合。

虽然我们的示例状态$|q_0\rangle$可以表示为叠加$|0⟩$和$|1⟩$，它和它们一样，是一个明确和定义良好的量子比特状态。为了看到这一点，我们可以开始探索如何操纵量子比特。

1.3使用 Qiskit 探索量子比特

首先，我们需要导入我们需要的所有工具：

在Qiskit中，我们使用QuantumCircuit对象来存储我们的电路，这本质上是我们电路上的量子操作以及它们所应用的量子比特的列表。

在我们的量子电路中，我们的量子比特总是以状态$|0⟩$开始。我们可以使用initialize()方法将其转换为任何状态。我们以列表的形式给initialize()我们想要的向量，并告诉它我们想在这个状态中初始化哪个量子比特:

然后，我们可以使用 Qiskit 的模拟器之一来查看量子比特的结果状态。

为了从我们的电路中获取结果，我们使用 run执行我们的电路，将电路和后端作为参数。然后，我们用.result()来得到这个结果：

从result中，我们可以使用.get_statevector()获得最后的状态向量：

Statevector([0.+0.j, 1.+0.j],dims=(2,))

注意： Python使用j来表示复数$i$。我们看到一个有两个复数元素的向量:0.+0.j = 0, 和 1.+0.j = 1.

现在让我们像在真正的量子计算机中一样测量我们的量子比特，看看结果：

这一次，我们不再使用状态向量，而是使用.get_counts()来获取结果0和1的计数:

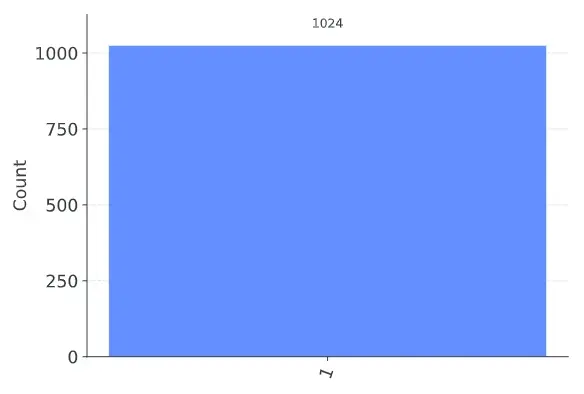
我们可以看到（正如我们所料），我们有100%的几率观察到$|1⟩$。这一次，让我们将量子比特置于叠加状态，看看会发生什么。我们将使用在前面提到的状态$|q_0\rangle$：

$$
|q_0\rangle = \tfrac{1}{\sqrt{2}}|0\rangle + \tfrac{i}{\sqrt{2}}|1\rangle

$$

我们需要将这些振幅添加到python的列表中。为了添加一个复数振幅，Python使用j作为虚数单位(我们在数学上通常称之为“$i$”):

然后，我们像以前一样重复初始化量子比特的步骤：

Statevector([0.70710678+0.j, 0.+0.70710678j],dims=(2,))

我们可以看到我们有相等的概率来测量|0⟩或|1⟩.为了解释这一点，我们需要谈谈测量。

2.测量规则

2.1一个非常重要的规则

测量有一个简单的规则。为了计算状态$|x\rangle$下$|ψ\rangle$的概率，我们这样做:

$$
p(|x\rangle) = | \langle x| \psi \rangle|^2

$$

符号 ⟨ 和 |告诉我们⟨x|是一个行向量，符号|和⟩告诉我们|ψ⟩是一个列向量。在量子力学中我们称列向量为kets,行向量为bras。它们一起组成狄拉克(bra-ket)符号。任何ket$|a\rangle$都具有相应的bra$\langle a|$，我们使用共轭转置在它们之间进行转换。

提醒：共轭转置（单击此处展开）提醒：内积（单击此处展开）

在上面的等式中，$|x⟩$可以是任何量子态。为了计算测量到$|x⟩$的概率，我们取$|x⟩$和测量到的状态(这里是$|ψ⟩$)的内积，然后进行平方。这可能看起来有点复杂，但很快就会成为你的第二感性。

如果我们观察之前的状态$|q_0⟩$，我们可以看到观测到$|0⟩$的概率确实是0.5：

$$
\begin{aligned}
|q_0\rangle & = \tfrac{1}{\sqrt{2}}|0\rangle + \tfrac{i}{\sqrt{2}}|1\rangle \
\langle 0| q_0 \rangle & = \tfrac{1}{\sqrt{2}}\langle 0|0\rangle + \tfrac{i}{\sqrt{2}}\langle 0|1\rangle \
& = \tfrac{1}{\sqrt{2}}\cdot 1 + \tfrac{i}{\sqrt{2}} \cdot 0\
& = \tfrac{1}{\sqrt{2}}\
|\langle 0| q_0 \rangle|^2 & = \tfrac{1}{2}
\end{aligned}

$$

您应该自己练习验证观测到$|1⟩$的概率。

这个规则支配着我们如何从量子态中获取信息。因此，它对我们在量子计算中所做的一切都非常重要。它也立即暗示了几个重要的事实。

2.2 本规则的意义

#1 规范化

该规则向我们表明振幅与概率有关。如果我们希望概率加起来为 1（他们应该！），我们需要确保状态向量被正确规范化。具体来说，我们需要状态向量的大小为 1。

$$
\langle\psi|\psi\rangle = 1 \

$$

因此，如果：

$$
|\psi\rangle = \alpha|0\rangle + \beta|1\rangle

$$

然后：

$$
|\alpha|^2 + |\beta|^2 = 1

$$

这解释了你在本章中看到的$\sqrt{2}$的因数。事实上，如果给initialize()一个未归一化的向量，它会报错:

错误输出

快速练习

1. 创建一个状态向量，该向量将给出$1/3$测量概率$|0⟩$。

2. 创建一个不同的状态向量，该向量将给出相同的测量概率。

3. 验证测量的概率$|1⟩$对于这两种状态是$2/3$。

你可以在下面的小部件中检查你的答案(答案精度为±1%，你可以在向量中使用pi和sqrt()等numpy术语):

#2 替代测量

测量法则给出了状态$|ψ⟩$被测量为$|x⟩$的概率$p(x)$。它没有告诉我们$|x⟩$只能是$|0⟩$或$|1⟩$。
到目前为止，我们所考虑的测量实际上只是测量量子比特的无数种可能方法中的一种。对于任意一对正交的状态，我们可以定义一种测量方法，让量子比特在这两种状态之间做出选择。
下一节将进一步探讨这种可能性。现在，请记住，$|x⟩$并不仅仅局限于$|0⟩$或$|1⟩$。

#3 全局相图

我们知道观测状态$|1⟩$将会带给我们确定性的输出 1。但是我们也同样能够将状态用这种方式书写：
$$
\begin{bmatrix}0 \ i\end{bmatrix} = i|1\rangle.
$$
为了了解它的行为，我们应用度量规则。
$$
|\langle x| (i|1\rangle) |^2 = | i \langle x|1\rangle|^2 = |\langle x|1\rangle|^2
$$
这里我们发现一旦取出复数的大小，因子$i$就消失了。这种效应与测量状态$|x⟩$完全无关。不管我们考虑的是什么测量，状态$i|1⟩$的概率与状态$|1⟩$的概率相同。由于测量是我们从量子比特中提取任何信息的唯一方法，这意味着这两种状态在物理相关的所有方面都是等效的。

更一般地说，我们将$|γ|=1$的状态上的任何总体因子$γ$称为“全局相位”。仅在整体阶段上存在差异的状态在物理上是无法区分的。
$$
|\langle x| ( \gamma |a\rangle) |^2 = | \gamma \langle x|a\rangle|^2 = |\langle x|a\rangle|^2
$$

请注意，这与叠加项之间的相位差不同，这被称为“相对相位”。一旦我们考虑不同类型的测量和多量子比特，这就变得重要起来。

#4 观察者效应

我们知道振幅包含了我们在特定状态下找到量子比特的概率信息，但一旦我们测量了量子比特，我们就确定知道量子比特的状态是什么。例如，如果我们测量状态中的量子比特:
$$
|q\rangle = \alpha|0\rangle + \beta|1\rangle
$$
在状态$|0⟩$中找到它，如果我们再次测量，有100%的机会在状态$|0⟩$中找到量子比特。这意味着测量的行为会改变量子比特的状态。
$$
|q\rangle = \begin{bmatrix} \alpha \ \beta \end{bmatrix} \xrightarrow{\text{Measure }|0\rangle} |q\rangle = |0\rangle = \begin{bmatrix} 1 \ 0 \end{bmatrix}
$$
我们有时将此称为量子比特状态的坍缩。这是一种强有力的效果，因此必须明智地使用。例如，如果我们不断测量每个量子比特以跟踪它们在计算中的每个点的值，它们将始终处于定义良好的$|0⟩$或$|1⟩$状态。因此，它们与经典比特没有什么不同，我们的计算可以很容易地被经典计算取代。为了实现真正的量子计算，我们必须允许量子比特探索更复杂的状态。因此，只有在我们需要提取输出时才使用测量。这意味着我们经常将所有的测量放在量子电路的末端。
我们可以使用Qiskit的状态向量模拟器来演示这一点。让我们初始化一个叠加态的量子比特:

这应该在状态中初始化我们的量子比特:
$$
|q\rangle = \tfrac{i}{\sqrt{2}}|0\rangle + \tfrac{1}{\sqrt{2}}|1\rangle
$$
我们可以使用模拟器验证这一点:

我们可以看到这里的量子比特初始化状态为[0.+0.70710678j 0.70710678+0.j]，这是我们所期望的状态。
现在让我们创建一个电路来测量这个量子比特:

当我们模拟整个电路时，可以看到其中一个振幅始终为0:

您可以重新运行此单元格几次，以重新初始化量子比特并再次测量它。你会注意到，任何一种结果都是等概率的，但量子比特的状态从来都不是$|0⟩$和$|1⟩$的叠加。有点有趣的是，状态$|0⟩$上的全局相位仍然存在，但由于这是全局相位，我们永远无法在真正的量子计算机上测量它。

关于量子模拟器的说明

我们可以看到，写下一个量子比特的状态需要跟踪两个复数，但当使用真正的量子计算机时，我们只会收到每个量子比特的是或否(0或1)答案。10量子比特量子计算机的输出看起来像这样:
$$
0110111110
$$
只有10位，没有叠加或复振幅。当使用真正的量子计算机时，我们无法在计算过程中看到量子比特的状态，因为这将破坏它们!这种行为对于学习来说并不理想，因此Qiskit提供了不同的量子模拟器:默认情况下，aer_simulator模拟真实量子计算机的执行，但如果我们在电路中包含某些指令，也允许您在测量之前查看量子状态。例如，这里包含了.save_statevector()指令，这意味着可以对模拟结果使用.get_statevector()。

3.布洛赫球

3.1 描述受限量子比特状态

我们在本章前面看到，量子比特（$|q⟩$）的一般状态是:
$$
|q\rangle = \alpha|0\rangle + \beta|1\rangle
$$
$$
\alpha, \beta \in \mathbb{C}
$$
(第二行告诉我们$α$和$β$是复数)。第2节中的前两个含义告诉我们，我们无法区分其中一些状态。这意味着我们可以更具体地描述量子比特。

首先，由于我们无法测量全局相位，我们只能测量状态$|0⟩$和$|1⟩$之间的相位差。我们可以将$α$和$β$限制为实数，并添加一个项来告诉我们它们之间的相对相位，而不是复数:
$$
|q\rangle = \alpha|0\rangle + e^{i\phi}\beta|1\rangle
$$
$$
\alpha, \beta, \phi \in \mathbb{R}
$$
最后，由于量子比特状态必须被规范化，即
$$
\sqrt{\alpha^2 + \beta^2} = 1
$$
我们可以使用三角恒等式:
$$
\sqrt{\sin^2{x} + \cos^2{x}} = 1
$$
为了用一个变量$θ$来描述真实的$α$和$β$:
$$
\alpha = \cos{\tfrac{\theta}{2}}, \quad \beta=\sin{\tfrac{\theta}{2}}
$$
从这里我们可以用两个变量$ϕ$和$θ$来描述任何量子比特的状态:
$$
|q\rangle = \cos{\tfrac{\theta}{2}}|0\rangle + e^{i\phi}\sin{\tfrac{\theta}{2}}|1\rangle
$$
$$
\theta, \phi \in \mathbb{R}
$$

3.2 直观表示量子比特状态

我们想绘制量子比特的一般状态:
$$
|q\rangle = \cos{\tfrac{\theta}{2}}|0\rangle + e^{i\phi}\sin{\tfrac{\theta}{2}}|1\rangle
$$
如果我们将$θ$和$ϕ$解释为球面坐标($r=1$，因为量子比特状态的大小是$1$)，我们可以在球面上绘制任何单个量子比特状态，称为布洛赫球。
下面我们绘制了状态中的量子比特$|+⟩$。在这种情况下，$\theta = \pi/2, \phi = 0$。

Qiskit有一个绘制布洛赫球的函数plot_bloch_vector()。这个函数默认接受笛卡儿坐标，但也可以通过传递参数coord_type='spherical'接受球坐标。
你也可以尝试这个交互式布洛赫球体演示。

注意

第一次学习量子比特状态时，很容易混淆量子比特状态矢量和它的布洛赫矢量。请记住，状态矢量器是1.1节中讨论的矢量，它保持了量子比特可能处于的两种状态的振幅。布洛赫球向量是一个可视化工具，它将2D、复杂的状态向量映射到真实的3D空间。

快速练习

使用plot_bloch_vector()绘制状态中的量子比特:

1.$|0⟩$

2.$|1⟩$

3.$\tfrac{1}{\sqrt{2}}(|0\rangle + |1\rangle)
$

4.$\tfrac{1}{\sqrt{2}}(|0\rangle - i|1\rangle)
$

5.$\tfrac{1}{\sqrt{2}}\begin{bmatrix}i\1\end{bmatrix}
$

关于Hacker Dōjō 

由Hacker共建的加密、Web3前沿技术开源知识社区。Dōjō 会以直播/音频/文字等形式定期组织分享session, 分享主题主要覆盖L1和L2的共识算法，架构，GitHub repo相关内容，包括不限于以下话题：Scroll / Polygon zkEVM、 Eigen的混合证明系统、Starkware、azTec、 Optimism、Zecrey、Aptos、 Move、密码学(零知识证明、公钥加密、哈希函数、格密码) 、 分布式系统、 以太坊协议栈、 量子计算和量子信息、卫星通信系统和航天器系统设计等。

✨Bounty详情及认领进度详情：https://innovative-laser af4.notion.site/174922df15884848b6ac8b57cb4f2fae?v=612e13dc6b9d44dd8197f755abb9fe9c

✨加入 Dōjō 中文社区微信联系：@HackerDojo0

有关DoraHacks

DoraHacks 是一个全球范围内的极客运动，全球黑客马拉松组织者，也是全球最活跃的多链 Web3 开发者平台之一。DoraHacks.io平台使得世界各地的Hacker和开源开发者可以参与黑客马拉松、Bounty、Grant、Grant DAO，以及公共物品质押等加密原生协议和基础设施进行协作并获得资助。到目前为止，DoraHacks 社区的 4000 多个项目已经获得了来自全球行业支持者超过 3000 万美元的资助。大量开源社区、DAO 和 超过50个主要区块链生态系统正在积极使用 Dora 的基础设（DoraHacks.io）进行开源融资和社区治理。

官网：https://dorahacks.io/