速成抢救:考研高数·经典函数之x^a*sin(1/x)

经学习发现，x^a*sin1/x是一个常考常用的初等函数。先摆结论：

1、a<0时

2、a=0时

sin(1/x)仍是个sin，它值域仍为[-1,1]，仍为奇函数。x=0处极限不存在，因为1/x在0处两侧极限为±∞，sin(∞)不存在，即原点处振荡频率无限大。sin(1/x)水平方向趋于0。

3、0<a<1:

无穷时仍趋于0，不用怀疑，怀疑的拿0/0未定式证一下子就行。虽然上图似乎衰竭的不够快，但：

4、a=1

它是个平喇叭，两侧水平渐近线y=1，因为无穷时有x*sin(1/x)=sin(1/x)/(1/x)=1,等价无穷小

5、1<a<2

喇叭口开始由平变为无穷，但都在y=x之下：

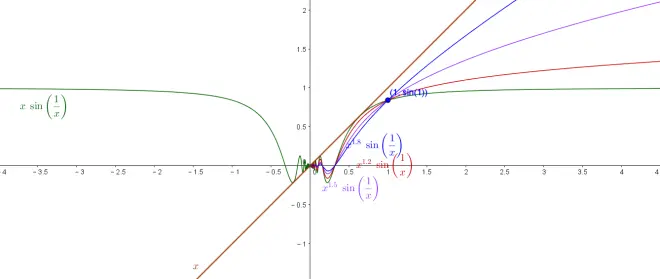
对于原点处：

因为在x→0时，sin(1/x)仍是个sin，值域仍为[-1,1]，所以sin1/x为有界振荡，而这些x^a（a>0）都是无穷小，∴无穷小乘一个有界量还是无穷小，函数x^asin(1/x)趋于0，即右极限=0。但x=0处受制于1/x的定义域，仍然是空定义点，所以我们会时常见到用花括号括起来的分段函数把这个可去间断点给填上f(0)=0。

6、a=2

它的图像有了更大的不同，它的斜渐近线是y=x。类推可得——

a=3时

随着幂次的升高，x^asin1/x图像形状开始主要受x^(a-1)支配。

总结自李永乐660：