【MC进阶命令】如何优雅地获取两点间距离?
本教程适用于Java 1.13+版本
什么是坐标?
要求两点间的距离,这两点肯定也有着相应的坐标,因此我们先从坐标看起
先以平面坐标为例
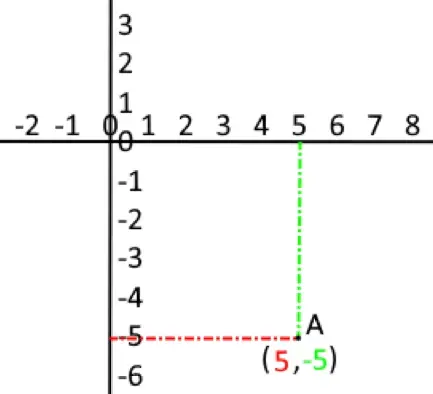
或许换一种方式更适合理解
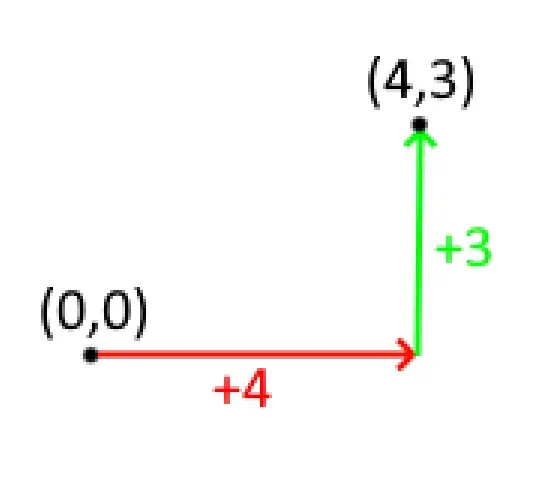
这种以原点(0,0)各轴延长一段正/负距离的坐标,被称为绝对坐标
再看看这张图:

先看黑色部分,这一部分的表示方法正是刚才讲到的绝对坐标的表示方法,但仔细看表示点A位置的橘色坐标与黑色坐标,这两个坐标并不一样,但表示的点却相同,它们之间的区别是什么呢?区别在于,橘色坐标是以另一个点(6,-2)延长而得到A的坐标的,获得的坐标也正是点A相对(6,-2)的坐标,这种相对的坐标,就叫做相对坐标
回顾一下:
绝对坐标:以原点(0,0)延长一定距离(分正负)得到的坐标,表示绝对的位置
相对坐标:以另一点延长一定距离(分正负)得到的坐标,表示一点相对另一点的位置
这时候可能有人要说了:要求两点间的距离,肯定求是连接两点的斜线,又不是两点的坐标差,讲这些有什么用呢?
欸,你先别急,才刚刚开始
三角函数!
看到“三角函数”四个大字先不要怕,其实很好理解
首先,在坐标系上,要表示斜线,其实就是表示一定比例的坐标

如图,x=2y形成了一条斜线,这意味着斜线上的每一点的x坐标与y坐标都满足2:1的关系,如图片中的一点(4,2),x坐标就是y坐标的两倍
现在,表示出一条斜线上的任意几个点的坐标,并观察这些坐标:

如图,表示P₁,P₂,P₃,P₄四个坐标的原点x轴延长线 y轴延长线 以及斜线本身构成了4个三角形:OP₁Q₁, OP₂Q₂, OP₃Q₃, OP₄Q₄,观察这些三角形,首先它们都是直角三角形,且其中三个三角形共用同一角,而剩下一个三角形的一角与前三个三角形共有的一角互为对顶角,因此四个三角形都是相似三角形
因此它们各自的三边(各自的x轴坐标 y轴坐标 以及对应的斜线的一部分)之间只有倍率关系,而不管哪一个三角形,x轴 y轴 斜边 这三边任意两个边的比值都是固定,即:
P₁Q₁ : OP₁ = P₂Q₂ : OP₂ = ... = 对边 : 斜边 = sin n (sin,全称sine,中文名正弦)
OQ₁ : OP₁ = OQ₂ : OP₂ = ... = 临边 : 斜边 = cos n (cos,全称cosine,中文名余弦)
P₁Q₁ : OQ₁ = P₂Q₂ : OQ₂ = ... = 对边 : 临边 = tan n (tan,全称tangent,中文名正切)
然而,这些函数名并不需要专门去记,只需要知道不同三角形的相同边的比值是相同的就行了
三角函数又该如何计算呢?可以让游戏帮我们算!
又是坐标?
在mc中,有三种坐标表示方法:
绝对坐标:直接使用坐标数值表示,例:tp 0 100 0 将会把执行者传送到0 100 0处
相对坐标:使用波浪号~加坐标数值,表示执行位置上的相对坐标,例:execute at @a run tp ~ ~1 ~ 将会让所有玩家传送到自己的位置向上1格处
#解析:execute是一条能够在修改执行信息 判断条件 储存返回值的情况下执行另一条命令的命令,execute中的at子命令能够将执行位置改为指定实体的位置,这里又联系到相对坐标的功能 “ 执行位置上的相对坐标 ” ,也就是修改了相对坐标判定的点为玩家的位置
局部坐标:使用我不知道叫啥的符号^加坐标数值,表示执行位置,执行方向上的相对坐标:

注:不纠正位置的情况下,局部坐标默认使用和相对坐标一样的脚部坐标(实际的坐标),而不是头部的坐标
例:execute at @a anchored eyes run tp ^ ^ ^1 将会让所有玩家朝视线前方传送1格
再注:就跟图片里的一样,“执行方向”与“局部z轴”是重叠的(为了看清除我特地拆开了,但其实是重叠的)因此视线前一格就需要表示为^ ^ ^1
再再再注:无论相对坐标还是局部坐标,只有在命令里使用的时候是存在的,最后改变的都是绝对坐标,例如tp到视线前方之后,你的坐标依然是绝对坐标
我们正好就可以用这个局部坐标计算三角函数:
梦幻联动!
现在终于可以开始看最初的问题了(喜
知道了斜边与另一边的比值是固定的,那我们就可以反过来用另一边的长度求斜边的长度了
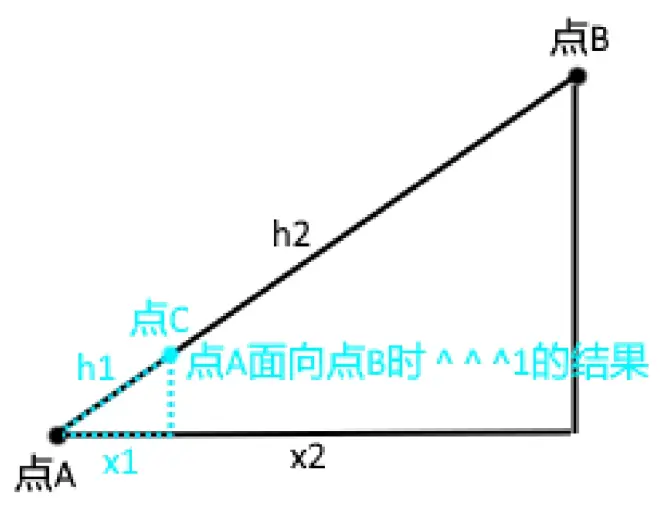
还记得最初的问题吗:获取两点间的距离
在这张图中,要获取距离的两点分别为点A 点B,而连接它们的斜线h2自然就是要求的距离了
而x2作为两点的x坐标的差,可以很简单地得到
再回顾一下刚刚讲到的局部坐标:表示执行位置,执行方向上的相对坐标,我们只要将执行方向设为在点A上面向点B的方向,并获取^ ^ ^1的x轴坐标,但是,此时获取的坐标是相对坐标转化为绝对坐标的值,要直接获取相对坐标,还需要将原位置移到原点(0,0,0)(这一步相当于减去了点A的坐标)再获取^ ^ ^1的x轴的值,此时的值才是x1的值,这时候可能就有人问了,h1在哪呢?哎,^ ^ ^1中的1就是h1的值啊!
再次观察图片,可以看到构成了一组与 “ 三角函数!” 部分一样的相似三角形,再根据该部分讲述到的三角函数知识,我们知道 cos A = 临边 : 斜边 = x1 : h1 = x2 : h2
现在结果已经显而易见了 x1 : h1 = x2 : h2 已知 x1 h1 x2 求 h2
很容易地就能算出,h2 = x2/cos A = x2/(x1:h1)
因为 h1 = 1 所以又可以简化为 h2 = x2 / x1
原理到这里就已经讲完了,现在只需要求得x2与x1即可
命令实现!
首先是获取x2 也就是点A 点B的x轴坐标差
十分的简单,先获取点A和点B的坐标,然后求差,这里可以先不取绝对值,后面再把h2取绝对值就行了
也就是获取 A的x坐标 - B的x坐标:
execute store result score #0 fTemp run data get entity 0-0-0-0-0 Pos[0] 1000000
execute store result score #1 fTemp run data get entity 0-0-0-0-1 Pos[0] 1000000
scoreboard players operation #0 fTemp -= #1 fTemp
(这里以实体0-0-0-0-0与实体0-0-0-0-1分别作为A和B,可自行换为目标选择器)
解析( 请自行省略其中的 “ < ” 和 “ > ” ):
execute store result score #0 fTemp run data get entity 0-0-0-0-0 Pos[0] 1000000
execute是一条以子命令为执行单位,能够在修改执行信息,判断条件,储存返回值的情况下执行另一条命令的命令
其中的store子命令可以将最后一个子命令的返回值储存在指定的位置,格式是 ... store <result>或<success> <位置> ...
当选择result模式时,会将储存命令的结果,而这里的“位置”,可以是一个计分板分数,格式如下:... score <分数拥有者> <计分项id> ...
而data get可以获取指定nbt的值,并返回这个值,而这个值,又刚好可以被execute store result储存,但由于store只能储存整型,计分板也只能记录整型数据,不能记录小数,因此要先进行放大再储存,以兼容小数,我这里乘上1000000(1000^2)是因为除数与商需要乘上1000倍,因此这里要乘1000^2倍
Pos是一个实体nbt,表示实体的坐标,Pos[0]则表示Pos数组中的第一项(也就是x轴坐标)
execute store result score #1 fTemp run data get entity 0-0-0-0-1 Pos[0] 1000000
这条跟上一条一样,只不过换成了另一个实体
scoreboard players operation #0 fTemp -= #1 fTemp
意思是计算减法 计算 #0 fTemp 减去 #1 fTemp 的值,并把计算结果储存在#0 fTemp里
最后得到的#0,fTemp就是x2的值了
然后是获取x1,这在前面已经讲过一次了
也不会多难,先在A的位置上把执行方向设为看向B的方向,然后讲执行位置设为(0,0,0)此时将临时实体tp到^ ^ ^1处,临时实体的x轴坐标就是x1的值了:
execute at 0-0-0-0-0 facing entity 0-0-0-0-1 feet positioned .0 .0 .0 run tp 0-0-0-0-2 ^ ^ ^1
execute store result score #2 fTemp run data get entity 0-0-0-0-2 Pos[0] 1000
(这里以实体0-0-0-0-2表示临时实体,可自行换成目标选择器)
解析( 请自行省略其中的 “ < ” 和 “ > ” ):
execute at 0-0-0-0-0 facing entity 0-0-0-0-1 feet positioned .0 .0 .0 run tp 0-0-0-0-2 ^ ^ ^1
又是熟悉的execute命令,这次先用execute中的at(修改执行位置)将执行位置改为了0-0-0-0-0(点A)的位置
随后用facing(效果是修改执行方向,格式是facing <坐标>或<entity 实体> <feet>或<eyes>,将执行方向改为看向指定实体或指定坐标时的方向)在这个位置上把执行方向改为了面向0-0-0-0-1(点B)的方向
又用positioned把执行位置改为了0.0,0.0,0.0(.0的写法省去了整数部分,默认为0)
最后把临时实体0-0-0-0-2传送到了以前面修改的方向上,局部坐标^ ^ ^1代表的位置
execute store result score #2 fTemp run data get entity 0-0-0-0-2 Pos[0] 1000
跟前面一样的获取坐标
最后得到的#2 fTemp就是x1的值了
这一大堆,说白了就是获取A面向B时^ ^ ^1转化为相对于A的位置时的x轴相对坐标
再说清楚点,就是点A朝点B移动一格,x轴增加了多少
最后计算 x2 / x1 的结果并取绝对值就行了
scoreboard players operation #0 fTemp /= #2 fTemp
把#0 fTemp的值设为#0 fTemp除以#2 fTemp的值
即 h2 = x2 / x1
execute if score #result fTemp matches ..-1 run scoreboard players operation #0 fTemp *= #-1 fInt
如果得到的数值为负数,则取相反数
最后的#0 fTemp就是两个实体间的距离啦
还可以加个tellraw @a {"score":{"name":"#0","objective":"fTemp"}}测试测试
要是有哪里不理解的可以来私信我
好了以上就是本教程的所有内容了,后面真的没有了,可以退出去了,不过看我写的这么认真可以给个三联或者评论下再退出去吗~ 啊不管给没给都谢谢啦~

