电路学习笔记44——复数

第八章 相量法

8-1 复数

1. 复数的表示形式

(1) 复数F的表示形式

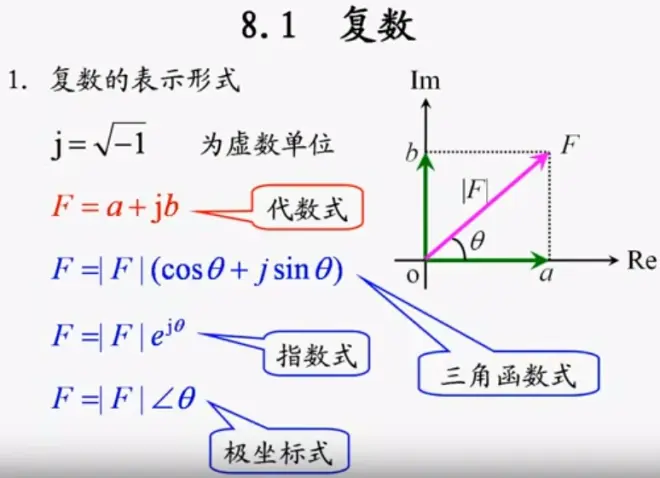
①　代数形式：F=a+jb，其中j=√-1，a=|F|cosθ称为实部，b=|F|sinθ称为虚部

②　三角函数形式：F=|F|(cosθ+jsinθ),其中|F|=√(a^2+b^2)称为模，θ=arctan（b/a）称为辐角

③　指数形式：F=|F|e^(jθ)

④　极坐标形式F=|F|∠θ

⑤　复数F在复平面上的表示如图。

(2) 一些复数的概念

①　取复数F的实部Re[F]=a；

②　取复数F的虚部Im[F]=b；

③　F的共轭复数（与F实轴对称的复数）F*=a-jb=|F|∠-θ。

2. 复数运算

(1) 复数的加减运算

①　复数的加减需在代数形式进行，若F1=a1+jb1,F2=a2+jb2，则F1±F2=(a1±a2)+(jb1±jb2)

②　复数的加减运算可按平行四边形法在复平面上用向量的相加和相减求得，如图所示。

(2) 复数的乘除运算

①　复数的乘除运算最好使用极坐标形式，若F1=|F1|∠θ1，F2=|F2|∠θ2，则F1*F2=|F1||F2|∠（θ1+θ2），F1/F2=|F1|/|F2|∠（θ1-θ2）

②　复数的乘除运算也可用代数式，具体如图。

③　若分母为一个复数，可将分子和分母同时乘以该复数的共轭复数来消除分母的虚部，使分母实数化。

(3) 旋转因子

①　任意复数乘以e^jθ等于把该复数逆时针旋转一个角度θ，而该复数的模不变，所以e^jθ称为旋转因子。

②　特殊旋转因子：+1=e^j0，-1=e^j±π，+j=e^j（π/2），-j=e^j（-π/2）

例：复数运算