向量数量积技巧大总结!投影!极化恒等式!拆解!

向量的数量积
00:26
描述两个向量相互作用产生的结果

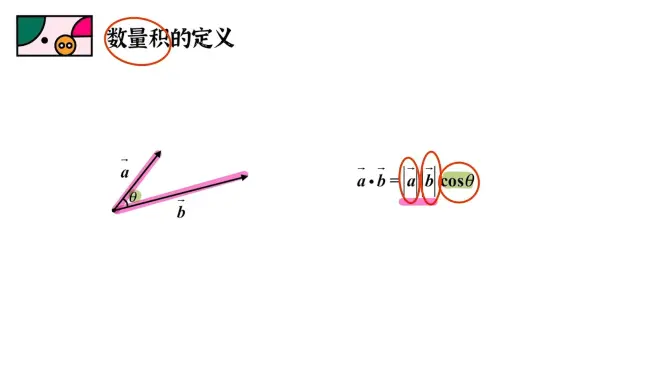
向量的大小和夹角(方向)有关
计算方法
02:14
将公式中的b的模长与夹角余弦值乘积看作一个整体,这个整体便是b向量在a向量上的投影长度。
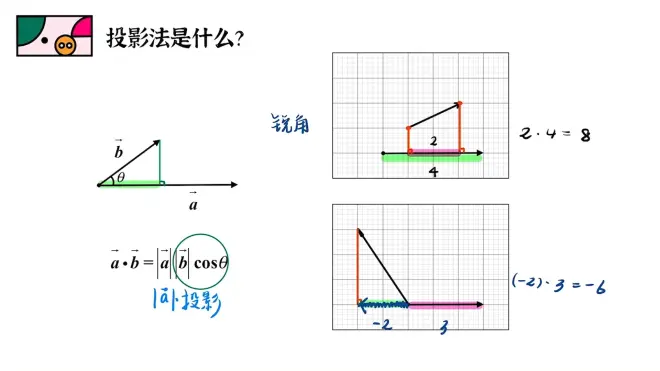
锐角→正值 钝角→负值

当一个变量固定不变时,可以使用投影法。

将动的向量向不动的向量投影

做题思路
①识别题型:向量的数量积
②选择方法:投影法
③计算:AB2不动,将别的向量投影

09:36


两个共起点的向量的数量积,底边固定

做题思路
①识别题型:向量的数量积
②选择方法:极化恒等式
③计算:设参量,解方程

15:47
内核:将求解的向量分解为已知的向量进行计算。
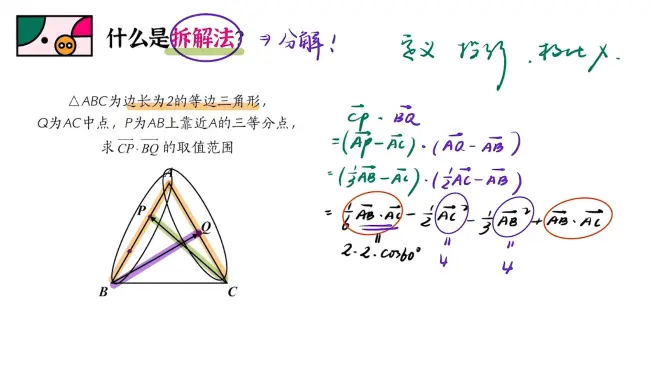
两向量横七竖八,用拆解法

选基底的原则



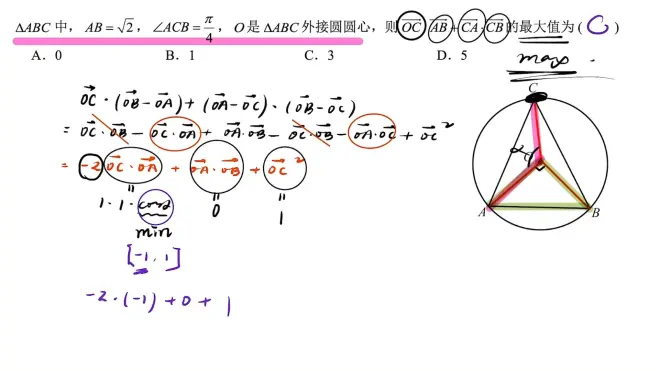
做题思路
①识别题型:向量的数量积的衍生
②选择方法:拆解法
③计算:找基底,求解数量积

小结:向量的数量积作为考试中经常出现的一种题型,虽然大部分都能做,但是选择使用相应简便的方法则会使计算又快又准。加油!

