双曲线方法、题型、性质，框架梳理！

题型和椭圆相似性很高（买一赠一）

双曲线公式和基本性质

渐近线记忆：分母是x的系数；分子是y的系数

别忘了正负

一。利用定义转换焦点的弦长

题目只连一个焦点时，一般会把另一个焦点连上👇

例题：做了一条辅助线，连接另一个焦点，就变easy啦

二。焦点三角形中点的问题

有些题目中会告诉你PF1的中点Q相关的性质

这类题基本会连OQ及PF2构造中位线

抛物线中同样适用

甚至有时可以自己构造中点

例题

复杂一些

两种情况都可以通过中位线解决

最后👇

三。解三角形法 （很多焦点三角形问题本质上都是几何问题，故可以通过正余弦定理来写）

构造方程的两种思路

1.已知焦点三角形任意一个角，并且剩余的三个边长都可以用abc表示出来（余弦）

例题

2。（麻烦一丢丢）双余弦法（本质就是解三角形问题）

如下的这几个边长可用a,b,c表示出来时，可用

例题

四。双曲线的计算方法

和椭圆一模一样 （后续视频会整理一些结论）

五。渐近线

1.会求渐近线

2.渐近线考法

①交点个数

如果问直线与双曲线有多少个交点，就需要渐近线来辅助理解

如：如果一条直线平行于渐近线，那么它与双曲线最多只能有一个交点

例题

②夹角范围

需要知道

Ⅰ.渐近线夹角的对称性

Ⅱ.夹角的大小

③特征三角形（以a,b,c三个长度形成的直角三角形）

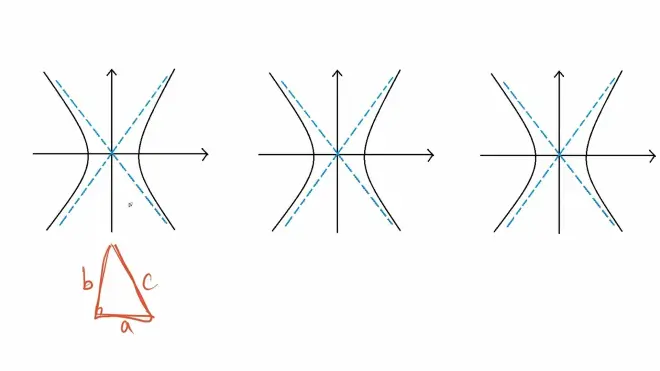
例题

如果是坐标运算（还挺麻烦）

六。常规条件的代数翻译（听话）

例题

总结：本节没讲的计算方法和椭圆更加类似，在大题中和椭圆几乎一模一样，后面视频会有结论