这是一道我作业中遇到的题。我的第一反应简直和答案完全一致：S甲=圆柱底面面积，S乙=一个宽不大于2r，长为h的矩形。

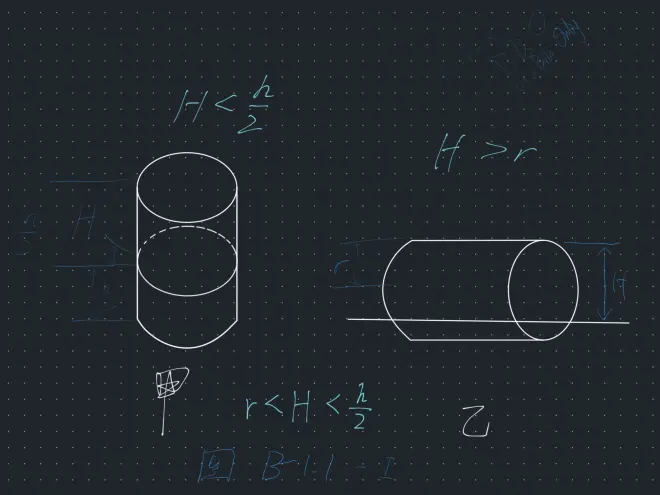
但因为直觉，我迟疑了一下Really???？我脑中第一时间呈现的是这张图

好，暂停一下，在具体解决问题之前，我们需要一些参数。

不妨设：r=甲乙圆柱半径,h=甲乙圆柱高,H=切去部分的高度

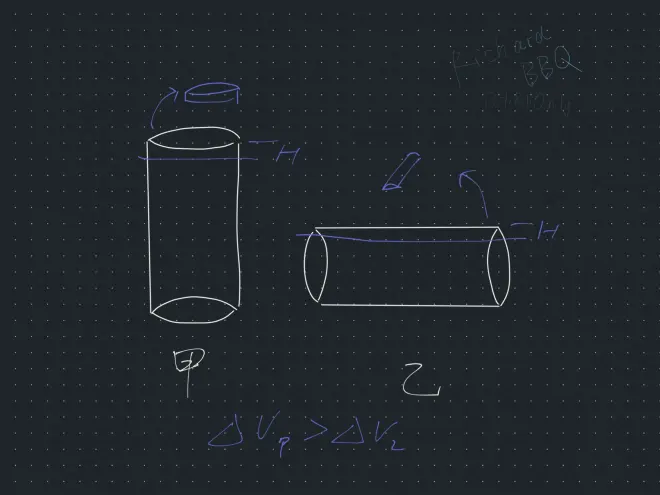
答案使用了体积公式:甲的体积并没有问题，但乙的切下部分从上到下不均匀。如果按答案的话算出的“ΔV乙”会比真实的“ΔV乙”大。所以S很明显并不是截面的那个矩形，而应该看成“月牙”的面积，高=h.

A-1:求S-思路

根据上述，主要问题已然明了：求“月牙”的面积S.

那么怎么求？半圆、圆的面积我们小学就学过，但这里的S是一个圆上用直线截下的一块。我们已经不能用初级方式去计算S了

求面积，在数学中有一个强大的工具：定积分。这时我们就应第一时间想到它，因为只要知道解析式、区间长就可以算出面积S。

A-2:求S-列式

首先我们要把整个圆放到平面直角坐标系中，用x轴截取S，这样比较方便。我们需要的差不多是这样一个东西(图A-2-I)

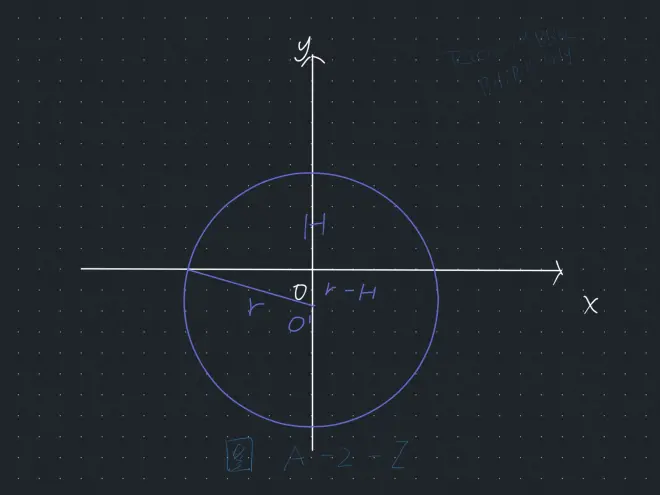
众所周知，圆的标准方程为

这里我们要让圆下移(r-H),因为“上减下加，左加右减”，则（PS:暂时先讨论切去的高不大于半径，其实算出这个，大于半径的也就显然了）

根据勾股定理，积分区间为

故

Emm…这个积分对于我还是有点难的

既然如此，不如将一个定积分拆解成拆成几个不定积分，然后逐个击破。

A-3:解S和ΔV乙

首先解第一项(∵r≥0,故原函数中的sgn(r)=1,省略)

代入，得

Step B-1:以具体数值比较ΔV甲与ΔV乙(H≤r,h=C_1,H=C_2)

根据上述，我们已知:

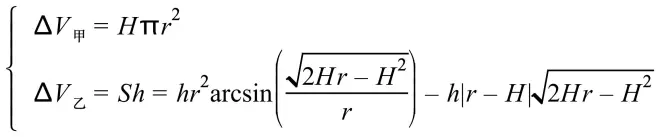
那么共有三个自变量:r=甲乙圆柱半径,h=甲乙圆柱高,H=切去部分的高度.和两个需要比较的因变量:ΔV甲,ΔV乙.本人能力有限，这步只能使用平面直角坐标系中的图像比较，即便如此，也需要剔除两个自变量，不妨先设H,h为常数。

y=ΔV>0,x=r>0,H=2,h=10,H=2≤r=x,即仅考察第一象限或特定区域的图像(下图设非蓝色区域为可行域)

为方便记忆，表达式很复杂的是ΔV乙，反之则是ΔV甲

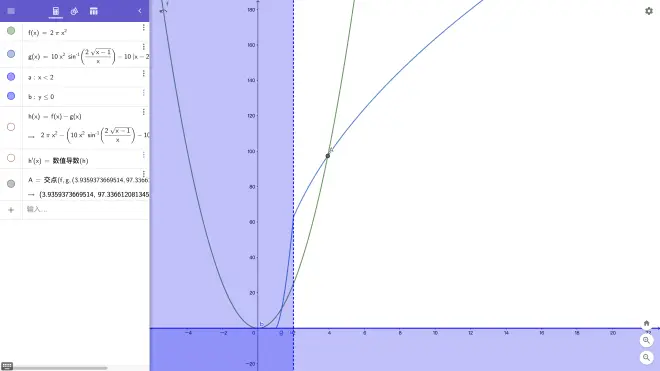
很明显的，当2≤r<3.935…时,ΔV甲<ΔV乙,符合题意;但当r≥3.935…时ΔV甲≥ΔV乙

Step B-1.1:小总结

到这里，我们成功证明了“题目有BUG”为真命题。但我们让“题目没有BUG”，方法一很简单：把“圆柱体”直接换成“矩体”。

方法二：不妨设ΔV甲<0.5V圆柱<ΔV乙.我形象地称其为“参数比较法”，这里我们就不需要ΔV的表达式，在这里，0.5V圆柱将成为“参照物”，让ΔV甲和ΔV乙与“参照物”比较，实现“曲线救国”(图B-1.1-I),可得当r<H<0.5h时,ΔV甲<ΔV乙

虽然我们以及找到并解决了BUG，但我认为我不该也不能止步于此。所以接下来，我们继续从数值比较，在慢慢找到三变量之间数量关系对ΔV的影响

我知道这将非常困难，让我直接解一个三元不等式是不可能的。接下来，必须全程依靠计算机的辅助

Step B-2:以具体数值比较ΔV甲与ΔV乙(H≤r,h=C_1,r=C_2)

同理，设 y=ΔV>0,x=H>0,r=2,h=10,H≤r=2,即仅考察第一象限或特定区域的图像

WOW!看来当”r,h”确定时,似乎是恒成立的

虽然很不明显，但当H很小时两者大小发生了变化；并且随H增大，差也会增大

Step C:标量场

(r,h,H)=>(x,y,z)

应该知道是什么意思

我也只是正为这个不等式发愁时偶然发现的标量场——一个似曾相识的名词

当研究物理系统中温度、压力、密度等在一定空间内的分布状态时，数学上只需用一个代数量来描绘，这些代数量（即标量函数）所定出的场就称为数量场，也称标量场(www.baidu.com)

也就是说，在某一空间区域中，物理量的无穷集合[此处为(r,h,H)]表示一种场

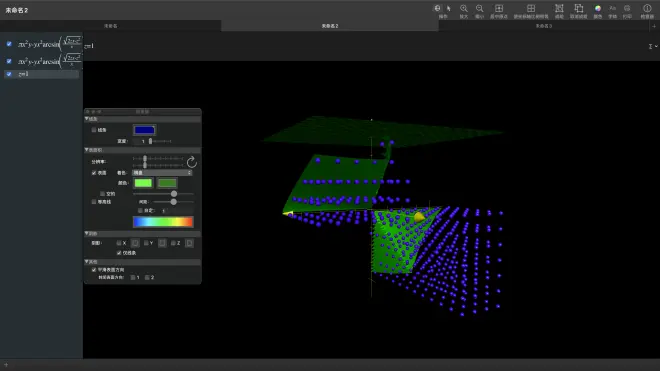
我们此处使用实标量场，仅考察第一卦限<=>(x,y,z)>0

此处用一个个紫色圆球表示标量场,最上方为z=1的平面，为演示单位长度，“覆盖”在球上的面为F(x,y,z)=0

TIP:实际上球应该是完全“覆盖”在“里面”的，可能是用球表示点集导致的渲染问题

现在我们还缺H>r的讨论，也没那么复杂，只需在ΔV乙的表达式中将H替换成(2r-H)即可

然后就会发现非常的amazing啊，这个式子是”轮换对称式”(并不符合严格定义，但有异曲同工之妙)

当H>r时,ΔV乙=V圆柱-ΔV乙(replaced)然后故计重施

整合

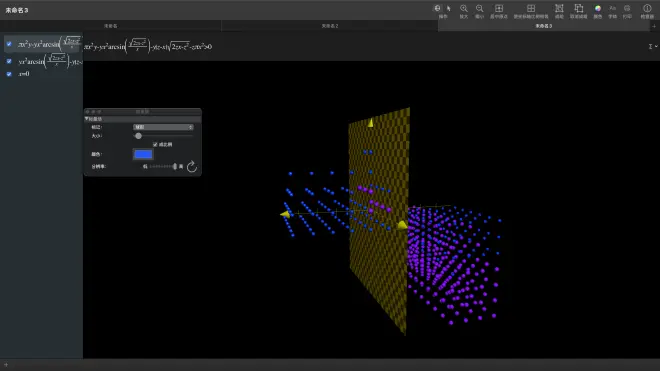
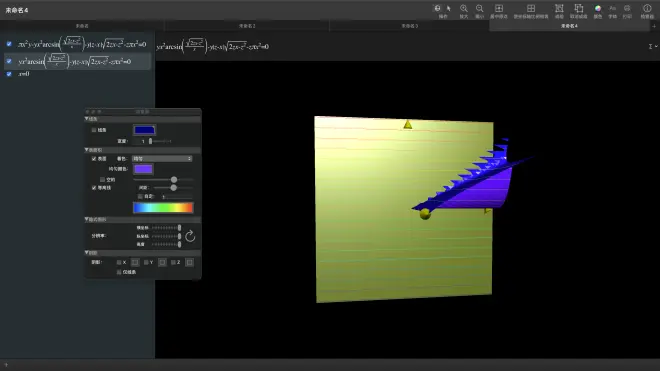
其实满足ΔV甲<ΔV乙的区域大概也就一半模样

D:总结

这个问题的后半(C)到这里也就不了了之，我不确定该不等式的解集，甚至不知道是否有明确的解集，像二元一次不等式用可行域表示也说不定。总之对于此，我想把这个问题留给以后

至于前半(AB)，我们也证明了“题目有BUG”并提出了改进方法，此处不多作说明。

……

再会。