3.2 标量场量子化（弯曲时空中二）

书接上回，上节中我们学习了一个标量场在弯曲时空中的量子化。并且定义了产生湮灭算符，由此首先可以定义真空态。通常都采用Rectangular坐标来，这些自然坐标适配到Poincare群。这使得Minkovski时空线元是不变的。具体的说，对时间t的偏导是一个Minkovski时空的Killing矢量，它是正交与类空超曲面的。并且(2.11)表示Killing矢量的本征态对应的本征值为i\omega（对于\omega大于0）。真空在Poincare来群的作用下是不变的。

在弯曲时空中，Poincaré 群不再是时空的对称群（参见 Urbantke 1969）。事实上，一般情况下根本没有Killing矢量来定义正频率模式。在某些特殊的时空类别中，可能存在某些受限变换下的对称性，例如旋转、平移或de sitter群。在这些情况下，可能存在与Killing矢量相关的 "自然 "坐标--类似于Minkovski空间中的矩形坐标。但即使存在这样的坐标，我们也会发现它们在量子场论中并不享有与Minkovski空间坐标相同的核心物理地位。事实上，广义相对论的整个精神，即通过广协方差原理表达的精神，就是坐标系在物理上是无关紧要的。坐标系统与物理无关。

因此我们可以考虑另一组解，并将场表示为：

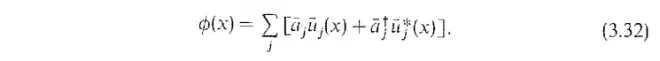
它可以定义新的真空和Fock空间：

可以利用Bogoliubov变换实现对两组解的变换：

其中\alpha和\beta是Bogoliubov系数，根据模式解的正交归一性，可以得到：

并且可以将这些转换到产生湮灭算符上：

并且， Bogoliubov系数有以下的属性：

这样可以明显的看出这两个Fock空间是不同的，例如：

(注意是a不能湮灭a杠所定义的真空态)。计算粒子数算符（a的）在另一个真空态下的期望值：

其中i表示第i个模式。这表示这个真空态在a看来不是空的(注意测量和被测量的关系）。

简单的总结一下就是，如果\beta=0时，这两个模式解所对应的真空是一样的。