无监督学习Kmeans聚类(代码重传

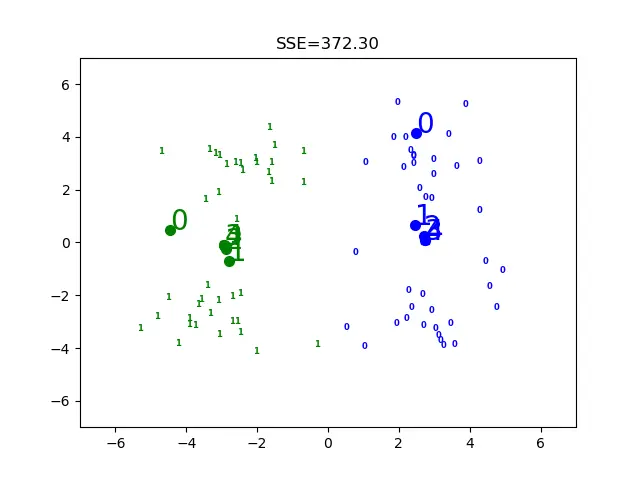
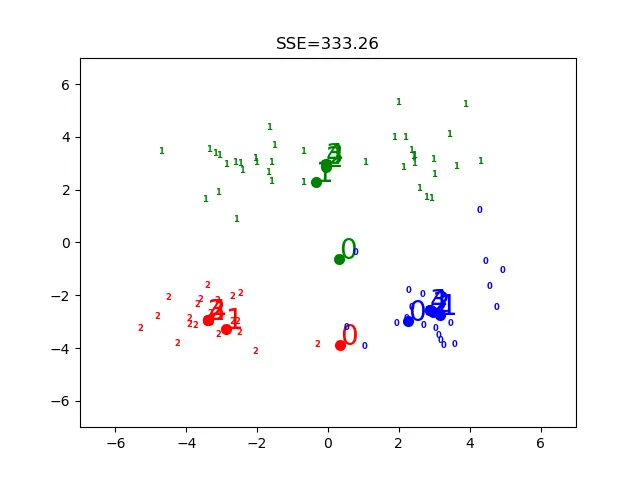
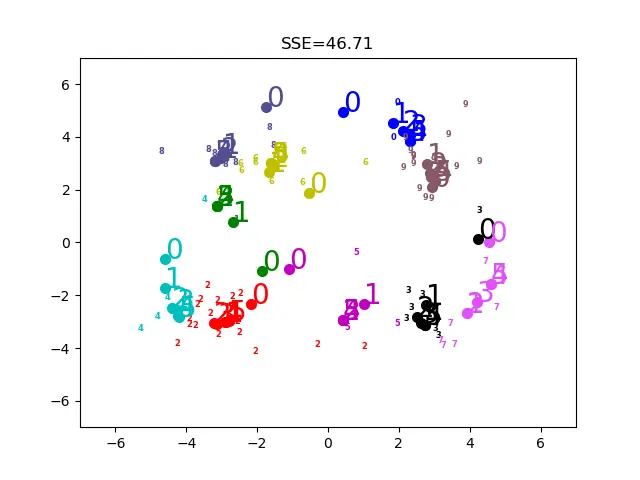
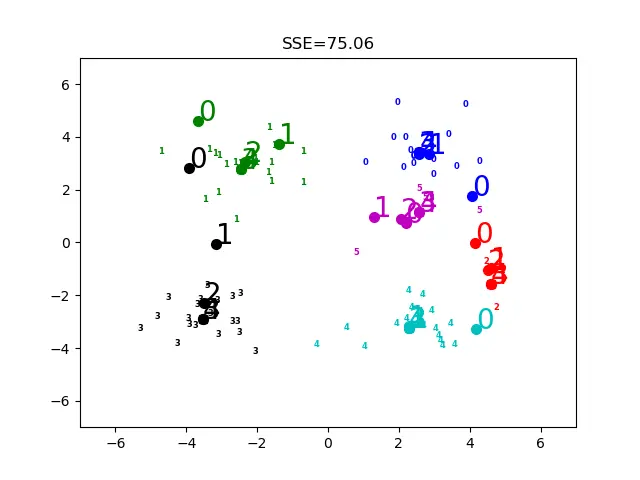
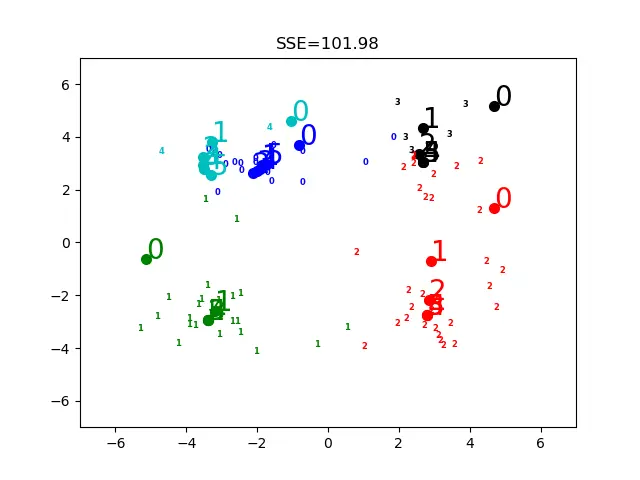
上面是k值不同时候的情况
共两个代码文件:
kmeans.py
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
class KMeansClassifier():
"""
这是一个kmean分类器
"""
# k initcent='random'初始化聚类中心的方法 max_iter=20训练的次数
def __init__(self, k=3, initcent='random', max_iter=20):
self._k = k # 接外面传进来的
self._initCent = initcent
self._max_iter = max_iter
self._clusterAssment = None
self._labels = None
self._sse = None
def draw_pic(self, step):
colors = ['b', 'g', 'r', 'k', 'c', 'm', 'y', '#e24fff', '#524C90', '#845868']
for i in range(self._k):
plt.scatter(self._centroids[i, 0], self._centroids[i, 1], marker='o', color=colors[i], linewidths=2)
plt.text(s=step.__str__(), x=self._centroids[i, 0], y=self._centroids[i, 1], color=colors[i], size=20)
# print(arrA, arrB) # 前一个是聚类中心的x y坐标,后一个散点的x y坐标 欧拉距离计算
def _cal_e_dist(self, arr_a, arr_b):
"""
功能:欧拉距离计算
输入:两个一维数组
"""
return np.math.sqrt(sum(np.power(arr_a - arr_b, 2)))
def _calMDist(self, arr_a, arr_b):
"""
功能:曼哈顿距离距离计算
输入:两个一维数组
arrA是聚类中心的x y坐标,arrB是散点的x y坐标
"""
return sum(np.abs(arr_a - arr_b))
# centroids[0][0]保存的是第一个聚类中心的x值 centroids[0][1]保存的是第一个聚类中心的y值
def _randCent(self, data_x, k):
"""
功能:随机选取k个质心
输出:centroids #返回一个k*n的质心矩阵
"""
n = data_x.shape[1] # 获取特征的维数
# print(n) # 这里是2,因为散点是二维的
centroids = np.empty((k, n)) # 使用numpy生成一个k*n的矩阵,用于存储质心坐标
for j in range(n):
min_j = min(data_x[:, j]) # 取到第j维最小的数
range_j = float(max(data_x[:, j] - min_j)) # 取到第j维的坐标变化范围
# 使用flatten拉平嵌套列表(nested list)
centroids[:, j] = (min_j + range_j * np.random.rand(k, 1)).flatten() # 随机选取第j维的坐标(保证坐标不超过数据)
# print(centroids)
"""
# 指定初始坐标
centroids = np.empty((k, data_x.shape[1]))
for i in range(k):
centroids[i][0] = i
centroids[i][1] = i
# print(centroids)"""
return centroids
# self._centroids[i, :] # 计算取出的第i类样本点的各个坐标均值
# self._labels # 样本点所属的类的索引值minIndex
# self._sse # 该点与其聚类中心的平方误差minDist**2
def fit(self, data_x):
"""
输入:一个m*n维的矩阵
本例是m*2
"""
if not isinstance(data_x, np.ndarray) or isinstance(data_x, np.matrixlib.defmatrix.matrix):
try:
data_x = np.asarray(data_x)
except:
raise TypeError("numpy.ndarray resuired for data_X")
m = data_x.shape[0] # 获取样本的个数m(79) data_X.shape[1]是维数n=2
# 准备一个m*2的二维矩阵,矩阵第一列存储样本点所属的类的索引值 第二列存储该点与其聚类中心的平方误差
self._clusterAssment = np.zeros((m, 2))
# 返回centroids[0][0]第0中心的x centroids[0][1]第0中心的y
if self._initCent == 'random':
self._centroids = self._randCent(data_x, self._k)
self.draw_pic(0) # =====================================================================================
# self._max_iter是最多训练的次数
for _iter in range(self._max_iter): # ============================对每次训练
shou_lian = True # 这个散点所跟随的聚类中心是不是变了
# 将每个样本点分配到离它最近的质心所属的族
for i in range(m): # ========================================对每个散点
min_dist = np.inf # 首先将minDist置为一个无穷大的数
min_index = -1 # 将最近质心的下标置为-1
# 次迭代用于寻找最近的质心
for j in range(self._k): # ===============================对每个聚类中心
# 第j个聚类中心的x y坐标 # ab第i个散点的x y坐标
arr_a = self._centroids[j, :]
arr_b = data_x[i, :]
dist_ab = self._cal_e_dist(arr_a, arr_b)
if dist_ab < min_dist:
min_dist = dist_ab # 更新
min_index = j # 记录
# 第一列索引值 第二列平方误差 共m行
if self._clusterAssment[i, 0] != min_index or self._clusterAssment[i, 1] > min_dist**2:
self._clusterAssment[i, :] = min_index, min_dist**2
shou_lian = False
if shou_lian: # 收敛,结束迭代
break
self.old_temp = []
# 更新 将每个类中的点的均值作为新的聚类中心的坐标
for i in range(self._k): # =====================================对于聚类中心数量
value = np.nonzero(self._clusterAssment[:, 0] == i) # 取出散点的索引值
self.old_temp[:] = self._centroids[i, :]
self._centroids[i, :] = np.mean(data_x[value[0]], axis=0) # 计算第i中心所有样本点的各个坐标均值
if self._centroids[i, 0] != self._centroids[i, 0]: # 是空值nan,没有人追随着个中心点
self._centroids[i, :] = self.old_temp[:]
# 这里打印出每步的聚类中心的位置
colors = ['b', 'g', 'r', 'k', 'c', 'm', 'y', '#e24fff', '#524C90', '#845868']
if _iter==0:
for i in range(self._k): # 对每个聚类
index = np.nonzero(self._clusterAssment[:, 0] == i)[0]
x0 = data_x[index, 0] # x坐标
x1 = data_x[index, 1] # y坐标
for j in range(len(x0)): # 对所有这些点
plt.text(x0[j], x1[j], str(i), color=colors[i], fontdict={'weight': 'bold', 'size': 6})
self.draw_pic(_iter+1)
self._labels = self._clusterAssment[:, 0] # 第一列存样本点所属的类的索引值minIndex
self._sse = sum(self._clusterAssment[:, 1]) # 第二列存该点与其聚类中心的平方误差minDist**2
# print('step', _iter, '\n', self._centroids, '\n', self._labels, '\n', self._sse)
# preds[:] 各个点依次的预测聚类中心
def predict(self, x): # 根据聚类结果,预测新输入数据所属的族
# 类型检查
if not isinstance(x, np.ndarray):
try:
x = np.asarray(x)
except:
raise TypeError("numpy.ndarray required for X")
m = x.shape[0] # m代表样本数量
preds = np.empty((m,))
for i in range(m): # 将每个样本点分配到离它最近的质心所属的族
min_dist = np.inf
for j in range(self._k):
dist_j_i = self._cal_e_dist(self._centroids[j, :], x[i, :])
if dist_j_i < min_dist:
min_dist = dist_j_i
preds[i] = j
return preds[:]
class biKMeansClassifier():
"""
这是一个二分 k-means
"""
def __init__(self, k=3):
self._k = k
self._centroids = None
self._clusterAssment = None
self._labels = None
self._sse = None
def _calEDist(self, arr_a, arr_b):
"""
功能:欧拉距离距离计算
输入:两个一维数组
"""
# print(arrA, arrB) # 前一个是聚类中心的x y坐标,后一个散点的x y坐标
return np.math.sqrt(sum(np.power(arr_a - arr_b, 2)))
def fit(self, X):
m = X.shape[0]
self._clusterAssment = np.zeros((m, 2))
centroid0 = np.mean(X, axis=0).tolist()
cent_list = [centroid0]
for j in range(m): # 计算每个样本点与质心之间初始的平方误差
self._clusterAssment[j, 1] = self._calEDist(np.asarray(centroid0), X[j, :]) ** 2
while(len(cent_list) < self._k):
lowest_sse = np.inf
# 尝试划分每一族,选取使得误差最小的那个族进行划分
for i in range(len(cent_list)):
index_all = self._clusterAssment[:, 0] # 取出样本所属簇的索引值
value = np.nonzero(index_all == i) # 取出所有属于第i个簇的索引值
pts_in_curr_cluster = X[value[0], :] # 取出属于第i个簇的所有样本点
clf = KMeansClassifier(k=2)
clf.fit(pts_in_curr_cluster)
# 划分该族后,所得到的质心、分配结果及误差矩阵
centroid_mat, split_clust_ass = clf._centroids, clf._clusterAssment
sse_split = sum(split_clust_ass[:, 1])
index_all = self._clusterAssment[:, 0]
value = np.nonzero(index_all == i)
sse_not_split = sum(self._clusterAssment[value[0],1])
if (sse_split + sse_not_split) < lowest_sse:
best_cent_to_split = i
best_new_cents = centroid_mat
best_clust_ass = split_clust_ass.copy()
lowest_sse = sse_split + sse_not_split
# 该族被划分成两个子族后,其中一个子族的索引变为原族的索引
# 另一个子族的索引变为len(cent_list),然后存入centList
best_clust_ass[np.nonzero(best_clust_ass[:, 0] == 1)[0], 0] = len(cent_list)
best_clust_ass[np.nonzero(best_clust_ass[:, 0] == 0)[0], 0] = best_cent_to_split
cent_list[best_cent_to_split] = best_new_cents[0, :].tolist()
cent_list.append(best_new_cents[1, :].tolist())
self._clusterAssment[np.nonzero(self._clusterAssment[:,0] == best_cent_to_split)[0], :] = best_clust_ass
self._labels = self._clusterAssment[:, 0]
self._sse = sum(self._clusterAssment[:, 1])
self._centroids = np.asarray(cent_list)
def predict(self, x): # 根据聚类结果,预测新输入数据所属的族
# 类型检查
if not isinstance(x, np.ndarray):
try:
x = np.asarray(x)
except:
raise TypeError("numpy.ndarray required for X")
m = x.shape[0] # m代表样本数量
preds = np.empty((m,))
for i in range(m): # 将每个样本点分配到离它最近的质心所属的族
min_dist = np.inf
for j in range(self._k):
dist_j_i = self._calEDist(self._centroids[j, :], x[i, :])
if dist_j_i < min_dist:
min_dist = dist_j_i
preds[i] = j
return preds
run.py
# -*- coding: utf-8 -*-
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from kmeans import KMeansClassifier
# 加载数据集,DataFrame格式,最后将返回为一个matrix格式
def loadDataset(infile):
df = pd.read_csv(infile, sep='\t', header=0, dtype=str, na_filter=False)
# print(df)
return np.array(df).astype(np.float)
if __name__ == "__main__":
data_X = loadDataset(r"data/testSet.txt")
# print(data_X[0][0]) # 是一个list,data_X[0][0]是第一个点的x坐标 data_X[0][1]是第一个点的y坐标
k = 4 # kmean的k
max_iter = 5 # kmean最大训练次数(100可以满足大多数要求)
clf = KMeansClassifier(k, max_iter=max_iter)
clf.fit(data_X)
labels = clf._labels # 由上一行计算得出
sse = clf._sse # 由上上一行计算得出
cents = clf._centroids # 由上上上一行计算得出
colors = ['b', 'g', 'r', 'k', 'c', 'm', 'y', '#e24fff', '#524C90', '#845868']
plt.title("SSE={:.2f}".format(sse))
plt.axis([-7, 7, -7, 7])
outname = "./result/k_clusters" + str(k) + ".png"
plt.savefig(outname)
# plt.show()
fig1 = plt.figure()
ax1 = fig1.add_subplot(111)
for i in range(k): # 对每个聚类
index = np.nonzero(labels == i)[0]
x0 = data_X[index, 0] # x坐标
x1 = data_X[index, 1] # y坐标
for j in range(len(x0)): # 对所有这些点
ax1.text(x0[j], x1[j], str(i), color=colors[i], fontdict={'weight': 'bold', 'size': 6})
ax1.scatter(cents[i, 0], cents[i, 1], marker='o', color=colors[i], linewidths=5)
plt.show()
# print('[[2, 2], [-4, -4]]两个点的预测结果=', clf.predict([[2, 2], [-4, -4]])) # 预测的输出
测试用的数据集
1.658985 4.285136
-3.453687 3.424321
4.838138 -1.151539
-5.379713 -3.362104
0.972564 2.924086
-3.567919 1.531611
0.450614 -3.302219
-3.487105 -1.724432
2.668759 1.594842
-3.156485 3.191137
3.165506 -3.999838
-2.786837 -3.099354
4.208187 2.984927
-2.123337 2.943366
0.704199 -0.479481
-0.392370 -3.963704
2.831667 1.574018
-0.790153 3.343144
2.943496 -3.357075
-3.195883 -2.283926
2.336445 2.875106
-1.786345 2.554248
2.190101 -1.906020
-3.403367 -2.778288
1.778124 3.880832
-1.688346 2.230267
2.592976 -2.054368
-4.007257 -3.207066
2.257734 3.387564
-2.679011 0.785119
0.939512 -4.023563
-3.674424 -2.261084
2.046259 2.735279
-3.189470 1.780269
4.372646 -0.822248
-2.579316 -3.497576
1.889034 5.190400
-0.798747 2.185588
2.836520 -2.658556
-3.837877 -3.253815
2.096701 3.886007
-2.709034 2.923887
3.367037 -3.184789
-2.121479 -4.232586
2.329546 3.179764
-3.284816 3.273099
3.091414 -3.815232
-3.762093 -2.432191
3.542056 2.778832
-1.736822 4.241041
2.127073 -2.983680
-4.323818 -3.938116
3.792121 5.135768
-4.786473 3.358547
2.624081 -3.260715
-4.009299 -2.978115
2.493525 1.963710
-2.513661 2.642162
1.864375 -3.176309
-3.171184 -3.572452
2.894220 2.489128
-2.562539 2.884438
3.491078 -3.947487
-2.565729 -2.012114
3.332948 3.983102
-1.616805 3.573188
2.280615 -2.559444
-2.651229 -3.103198
2.321395 3.154987
-1.685703 2.939697
3.031012 -3.620252
-4.599622 -2.185829
4.196223 1.126677
-2.133863 3.093686
4.668892 -2.562705
-2.793241 -2.149706
2.884105 3.043438
-2.967647 2.848696
4.479332 -1.764772
-4.905566 -2.911070

