质数计数函数与黎曼 zeta 函数的关系以及其显式形式 [上]
众所周知, Reimann ζ 的零点与质数有着密不可分的关系, 其中最直接的就是质数计数函数 π(x) 可以由 ζ 的零点表示, 质数计数函数就是给出小于等于 x 的质数的数量, 比如 π(10) = 4, 因为小于等于 10 的质数有 4 个: 2, 3, 5, 7, 注意 π(x) 的 x 不只是整数, 对于任意正实数都是可以的, 下面是 π(x) 的 1~100的图像:

可以看到随着 x 的增加, 遇到一个质数时 π(x) 的值就会增加 1 (废话). 但实际上由 ζ 的零点给出的显式形式并不是 π(x), 而是一个稍微"圆滑"一点的函数 π₀(x), 这个函数随着 x 的增加遇到质数时, π₀(x) 只会增加 0.5, 随后才会再增加 0.5, 也就是说 π₀(x) 在质数处只会取到半整数而不是整数, 如下图所示:

这种奇怪的跳一半的性质对于熟悉 Fourier 变换的人来说一定很熟悉, 在这里的原因也是类似的. 在开始计算之前, 下面介绍符号以及引入另外几个与质数密切相关的函数

符号 & 函数
符号 表示质数, 并且
表示 p 取全体质数的求和符号. 那么质数计数函数写成式子为
.
符号 表示 ζ 的零点 (平凡的和非平凡的), 类似地,
表示 ρ 取全体 ζ 零点的求和符号. 另外, 因为平凡零点的实部总是小于 0, 非平凡零点的实部总是大于 0, 所以使用
分别表示平凡零点和非平凡零点.
第一个引入的函数是 von Mangoldt 函数 Λ, 其定义如下:
也就是当整数 x 是某个质数 p 的次方数时, Λ(x) 为 p 的自然对数, 否则为 0.
第二个引入的函数是 Chebyshev 函数 ψ, 其定义如下:
也就是 ψ 是 Λ 的求和函数, ψ 存在一种等价的定义: 在给出 p 和 x 时有 x = p^k, 那么小于等于 x 的 "p 的次方数" 的数量为 ⌊k⌋, 其中 ⌊·⌋ 为向下取整函数, 那么 ψ 可以定义为 , 下图是 ψ(x) 的 1~100 的图像.

另外, ψ 也存在"圆滑"的版本 ψ₀, 与 π₀ 类似, 这个函数在进行"跳跃" 时会分为两次"跳跃". 并且 π₀ 和 ψ₀ 都可以通过下式定义, 其中 f 为 π 或 ψ
在进行函数的积分变换时就会出现这种情况, 这里以 Fourier 变换为例, 但这对于下面提到的 Mellin 变换也是一样的.
由 π 和 ψ 的定义可以知道, π(1) = ψ(1) = 0, 这个性质在下面将会非常重要.

质数定理 & 黎曼猜想
质数定理描述的是随着数字增大时质数分布的情况, 第一个估计由下式给出:
对上式的另一种描述是 . 这个式子表示随着 x 的增大, 质数计数 π(x) 会趋向于 x / ln x. 另一个更好的估计由下式给出:
其中 li 是对数积分函数 , 很多地方会使用另一个有略微不同的对数积分函数 Li(x) = li(x) - li(2), 不过这个常数对 x → ∞ 时没有影响. 两种估计的相对误差如下图所示:

虽然质数定理存在初等证明但是非常繁琐, 又存在简短但使用柯西积分定理的证明, 但是这里既然提到了 ζ 零点以及 Chebyshev 函数, 那么下面将使用这两个来证明质数定理.
首先, 质数定理 等价于
, 如果后者成立, 那么质数定理也成立.
证明等价性: 由 ψ 的定义得
然后对于任意 0 < ε < 1 有
将上式两边同除以 x 得
当 x → ∞ 时 x^{ε-1}*ln x → 0, 即
综合上面两个结论得 , 即
, 那么如果质数定理成立, 则有 ψ(x) ~ x, 反之亦然.
然后证明 ψ(x) ~ x:
首先 ψ 有以下显示形式 (后文有给出):
正如符号约定里面说的, ρ₊ 表示 ζ 的非平凡零点. 当 x → ∞ 时, 1/2 * ln(1-x⁻²) → 0, 那么如果 ψ(x) ~ x, 则上式求和部分的增长速度小于 x.
设 Re(ρ₊) = σ, 可以知道求和内的增长速度受限于 x^σ, 那么求和部分的增长速度受限于 , 其中 σₘₐₓ 为所有非平凡零点里最大的实部, 在前前篇文章里有证明过: ζ 非平凡零点只在 0 < Re(s) < 1 里, 也就是说 σₘₐₓ < 1, 亦即证得 ψ(x) ~ x, 从而证明了质数定理.

实际上有 , 但是证明这个式子有亿点复杂, 而且跟上面的理念差不多. 因为质数定理与 ψ(x) ~ x 等价, 而 ψ(x) - x 的增长速度与 x^σₘₐₓ 有关, 当黎曼猜想成立时 (即 σₘₐₓ = 1/2), 可以得出结论
(Schoenfeld, 1976).
·

更多符号 & Mellin 变换
定义 Identical 函数 I(s) = s, 因为接下来需要使用大量函数变换算符, 所有这里先定义好这堆算符:
U 算符:
R 算符:
D 算符:
× 算符:
∘ 算符:
算符的运算都是从右到左的: 和
, 定义这堆算符是为了将函数变换从具体的函数参数里摆脱出来, 使得式子更简洁. 由 R 算符的定义可以知道有
, 证明:
.
接下来引入一个重量级工具: Mellin 变换, 其定义如下:
其逆变换为:
这里并不打算讨论逆变换这一坨是什么东西, 毕竟这里不是复分析教程.
Mellin 变换与上面的算符组合可以产生一些结论:
1.
2.
证明:
1.
2.
因为 U 算符把被积部分在 t < 1 时都变成了 0, 所以有
应用分部积分 , 得
当 Re(s) < 0 和 f(1) = 0 时, 上式左边为 0, 那么得

Λ 与 ζ 的联系
Λ 与 ζ 有 , 证明:
注意到 , 那么
代入 ζ 的欧拉乘积形式
Taylor 展开 得
由 Λ 的定义可得

ψ 与 ζ 的联系
不难知道 , 证明:
那么 ψ 与 ζ 有 , 证明: 由 Λ 与 ζ 的联系得
另外有 , 并且对于正实数 x 有
, 那么
根据 ψ 的定义, ψ(0) = 0, 所以 Uψ = ψ, 那么上式的积分下限可以变为 0, 使用 -s 替换 s 上式得到
证毕. 另外这个联系可以写为与参数无关的形式 , 应用上面列出的算符运算, 得到
.

ψ 的显式形式
实际上有了上面的关系之后, 熟悉复分析的人就可以用 Mellin 逆变换开始嗯算了, 但是这里进行一个巧的取.
Hadamard 根据 Weierstrass 分解定理给出了 ζ 的一种表达形式
其中 ρ 为 ζ 的全部零点. 尽管这里不会证明这个表达式, 但是可以描述一下 Weierstrass 分解定理:
首先复习代数基本定理: 一个 n 次多项式 必定存在 n 个零点, 如果将第 j 个零点记为 ρⱼ, 那么这个多项式可以表示为
.
那么 Weierstrass 分解定理可以看作代数基本定理的扩展: 任意整函数都可以表示为与其零点相关的函数的乘积. 假设整函数 f(s) 的第 j 个非零零点为 ρⱼ (如果零点的阶 k > 1, 那么重复出现 k 次这个零点), 并且 f 在 s = 0 为 m 阶零点 (m = 0 表示 0 不是 f 的零点), 那么则存在整函数 g(s) 和一系列整数 bⱼ 使得 , 其中
.
有了 Hadamard 乘积形式后可以开始计算:
首先对于 Re(s) < Re(a) 有 , 证明:
其次有 , 然后
将 Hadamard 乘积形式代入:
其中 1/ρ + 1/(s-ρ) = s / (ρ(s-ρ)), 并且 1 + 1/(s-1) = s / (s-1), 然后得到:
应用 得
由积分的线性可以知道 Mellin 变换也是线性的, 对比上式可以得出
假设 x > 1, 然后把上式的求和部分的零点分为平凡零点和非平凡零点, 因为平凡零点为全部负偶数, 所以
并且有 Taylor 展开 那么得到
另外一点比较有趣的是可以把 x 看作 x¹ / 1, 这个形式与上面的零点求和内是一致的, 但是与零点求和异号 (x 符号为正, 零点求和为负), 这是因为 1 是 ζ 的一阶极点, 并且 , 也就是说 ψ 与 ζ 里的零点, 极点和 0 有关 (从 Weierstrass 分解定理也可以直接看出这点).
既然求得了显式形式, 那当然要来看看图片的:

上图是使用了 ζ 的前 100 个非平凡零点 (Im(ρ) > 0) 产生的图像, 可以看到在值较小时, 显式形式的 ψ₀ 以及很好地与 ψ₀ 重叠了起来, 但在值较大时还需要更多数量的零点才能足够接近, 下面是使用前 25000 个非平凡零点得到的绝对误差:
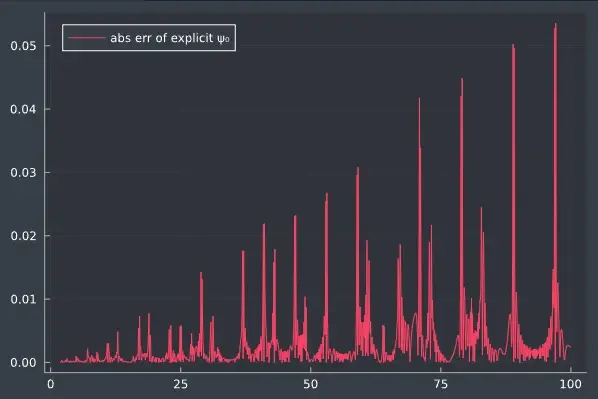
图中的尖刺产生的原因正是因为积分逆变换不能很好地在函数"跳跃"处收敛, 其他地方都已经有很好的接近了.

(接下篇)

