[中英字幕]吴恩达机器学习系列课程

机器学习的三个阶段:
经验E:和程序员下几万盘棋、观察是否将邮件标为垃圾邮件
任务T:下棋、判断邮件是否为垃圾邮件
性能度量P:棋局是否胜利,正确将垃圾邮件归类的数量
机器学习算法:
监督学习、无监督学习
监督学习:给出数据集
- 回归问题:连续,针对大批量进行预测
- 分类问题:离散,针对单个。。。。。
无监督学习:没有给出数据集的正确答案(未辨别数据类型)
- 聚类算法:将已分类的信息分成“簇”
- 鸡尾酒会算法:将混杂的信息分离出来
在学习后,将得出一个假设函数h:输入平米数可得出房价
线性回归:将数据拟合成线性函数

代价函数:平方误差函数
目的是找出代价函数最小时的θ1、θ0
通过代价函数的表达式可以看出,当代价函数最小时,拟合程度最好。

梯度下降法:用来计算代价函数最小值
α:学习率,控制以多大幅度更新参数θ
与α相乘的偏微分决定了移动的方向始终是向下的
针对线性回归的梯度下降算法:h(x)=θ0+θ1*x

h(x)=(θ^T)*x θ,x均为n维向量
多元线性回归,利用多个特征值来预测
多元梯度下降法:x变为向量。
为了让梯度下降更快的两种方法:
- 特征缩放:有时代价函数会变成细长的椭圆形,下降就会曲折缓慢,通过计算将特征值的范围缩小到*(0,1)会使椭圆接近正圆,下降就会变得快速。
- 均值归一化:0<size<2000,1<bedrooms<5

x1:=(x1-μ1)/s1
x1:特征值。μ1:特征值平均值。s1:特征值范围
当学习率α
过小时:迭代会很慢
过大时:J(θ)可能不会每次迭代都下降,也可能不收敛。
解决方法:绘制J(θ)的图像、观察。
计算θ的方法
- 梯度下降法:需要选择α,需要迭代,当维度很大时仍然好用
- 正规方程法:n大于10000时效果不好

X数据集中的特征值组成的向量
y数据集中的输出组成的向量

不可逆的原因:
- 特征值线性相关,删掉多余的。
- 太多的特征值,删掉一些,或者正规化。
关于分类的问题一般不用线性回归算法
Logistic Regression:分类算法
让假设函数的范围限制在(0,1)
0<=h(x)<=1
logistic算法:
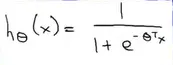
h(x)=P(y=1|x;θ)
代表着当输入为x时,y为1的概率,这个概率的参数时θ
决策界限:区分y=0,y=1的线
logistic回归的代价函数:

用梯度下降法拟合logistics回归的参数
logistics回归:

一对多问题:将多个问题化为多个独立的二元问题,也就是有多个分类器y=i(y实际值,i预测值),把x输入到多个分类器中,哪个概率最高就是哪个类。

当用过高阶次的多项式拟合,就会出现过拟合(图三)
解决方法:
- 减少特征变量
- 正则化
正则化

λ:正则化参数,过大将导致对每个参数的惩罚过大,θ=0.
Σ(θ^2):正则化项,缩小每个参数

正则化后的线性回归相当于把参数乘以一个比1小一点的数 (1-α(λ/m))<1
神经网络可以实现逻辑运算
δ(l)j:l层节点j的误差
a(l)j:l层单元j的激活值
梯度检测:用来验证反向传播算法

如果权重都为0的话,hθ只能得到一个特征
所以要将权重θ随机初始化在[-ε,ε]。
- 训练神经网络:
- 将θ随机初始化在[-ε,ε],接近于0
- 进行前向传播算法得到h(θ)
- 计算J(θ)
- 进行反向传播算法算出J(θ)的偏导
- 梯度检查
- 使用最优化算法
解决高方差
- 收集更多数据,
- 选用更少特征以减少过拟合
- 增加λ
解决高偏差
- 更多特征
- 增加多项式特征(x^2,x1x2)
- 减小λ
线性回归的测试
- 从训练集中得到θ
- 计算误差

分类问题的测试
- 得到θ
- 计算误差

错误分类误差

模型选择:选择合适的多项式
60%:40%分成训练集和测试集
通过测试机选择多项式的次数,然后仍在测试集上计算误差会出现问题,所以要分为:
60% :20% : 20%
训练集 交叉验证集 测试集

高偏差(欠拟合):
Jcv,Jtrain都很大
高方差(过拟合):
Jcv>>Jtrian
选择正则化参数λ 0 0.01 0.02 0.04 0.08 ........10.24共12个
带入每个λ最小化J(θ)以得到θ
用验证集评价,得出每个θ在验证集上平均的误差平方和
选最小的误差平方和对应的θ1
观察θ1在测试集上的表现
算法处于高方差时的特点:Jcv误差和Jtrain误差相差很大

。。。。。误差。。。。:。。。。。。。。。在足够多样本时相差不大


