心血管支架疲劳性能的有限元分析
针对支架的拉伸疲劳性能进行了有限元分析,设计了一套有效的模拟过程去分析支架在不同直径以及不同拉伸应变下的表现,并且应用等效应力(SEQA)去评估支架的拉伸疲劳性能。SEQA显示了和VonMises应力完全不同的结果。此外,利用Goodman图对支架的疲劳破坏进行预测。结果显示,支架将发生破坏。5
关键词:血管支架;有限元;拉伸疲劳
心血管疾病是全世界面临的可导致死亡的最普遍疾病之一,其中血管阻塞是罪魁祸首。血管支架疗法是对血管阻塞进行有效修复的治疗方法。在美国,每年有几百万的血管支架被植入人体中。尽管血管支架得到了广泛应用,但是支架在植入后发生的破坏问题还没有得到解决。支架的力学性能在这个问题中扮演了关键性的角色,因此对支架力学性能的研究十分重要[1]。有限元分析可有效分析支架的力学性能,很多研究针对可能影响支架力学性能的因素进行了有限元分析。一些研究分析了在支架扩张过程中气囊对支架的影响[2],还有一些研究分析了支架和血管的相互作用[3-4]。但是,针对支架扩张后的疲劳性能的研究更为重要。
实际上,支架在植入后承受着轴向周期应变。因此,针对支架的拉伸疲劳性能的研究十分重要。与此同时,支架扩张后的直径对拉伸疲劳性能有显著影响。本研究的目的是分析支架的疲劳力学性能。有限元分析被用在了支架的应力状态分析中,通过等效应力计算的Goodman图被用于预测支架在轴向应变条件下是否会发生破坏。
1 实验方法
1.1 支架模型
由图1(a)所示,通过有限元分析软件Abaqus6.09进行了S-stent(BiosensorsInternational)支架的建模。模型的尺寸通过S-stent的SEM照片得到。为精简模型,考虑到支架在轴向和圆周方向的对称性,将1/4模型应用于研究。
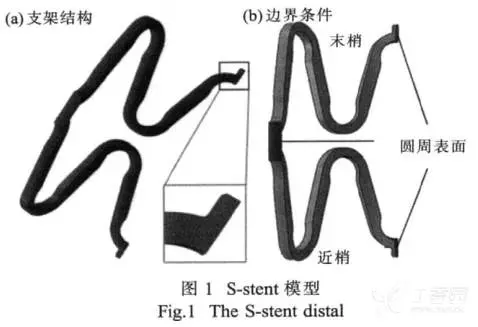
支架的材料是SUS316L不锈钢,在模型中支架材料被设定为均匀、各向同性、具有弹塑性。其中弹性模量为193GPa,泊松比为0.3,真实应力应变曲线用于描述材料塑性区域的应力应变关系[5-6]。
1.2 边界条件
模型的初始直径为2.8mm,它经历了卷曲(将支架收缩附着于气球表面这个过程)、扩张、拉伸疲劳三个过程。其中,卷曲是为了引入在支架生产过程中的残余应力。
步骤一:卷曲。固定支架尾端,在其外表面施加均匀的位移,使支架的直径从初始的2.8mm变为1.2mm。
步骤二:扩张。固定支架尾端,通过控制支架内表面的位移,使支架扩张到不同的直径(3.0、4.0和5.0mm)。随后消去位移控制,模拟实际过程中撤去气球后支架在直径方向的回弹。
步骤三:拉伸疲劳。固定支架尾端,在支架顶端施加轴向位移,进行拉伸过程的模拟。首先,针对不同的最大应变(εmax=0.2、0.15和0.1),施加相应的最大位移于支架尾端。其次,根据疲劳条件(εmin/εmax=0.1),撤去初始位移,施加数值等于最大位移10%。最后,重复以上两个过程一个周期。
如图 1(b) 所示,在以上所有过程中,圆周方向对称的边界条件一直被施加于支架上。并且为防止刚性位移,支架尾端也被一直固定。

2 实验结果与分析
2.1 应力分析
在拉伸疲劳过程中,支架(最大应力处)所经受的轴向应力路径由图2所示。由于模拟了卷曲过程,支架的初始应力为407MPa。在随后的拉伸疲劳过程中,支架所经受的轴向应力在608~539MPa。在此之后,持续了一周期的拉伸模拟。结果显示,支架所经受的轴向应力重复了前一个周期的路径。这表明本研究的模拟法可有效反应支架长期的拉伸疲劳应力状况。
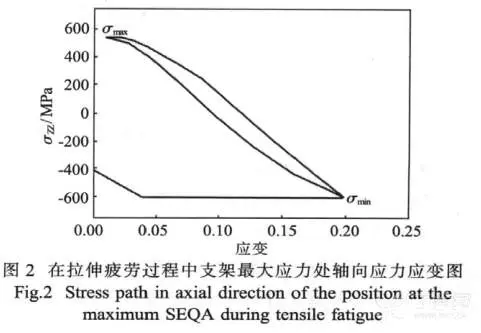
在最大应力为0.2时,支架模型的Goodman结果由图3所示。模型中所有的节点都绘制于Goodman图中,其中落于Goodman直线左下方的点表明这些位置在拉伸疲劳的条件下是安全的。相反,落于Goodman直线右上方的点表明这些位置可能发生疲劳断裂。为了量化Goodman图中每一个点的安全状况,每一个点和Goodman直线的距离可转化为该点的安全系数。如果落于安全区域,该点离Goodman直线的距离越远,则说明该点越安全。如果落于危险区域,该点离Goodman直线的距离越远则说明该点越危险。
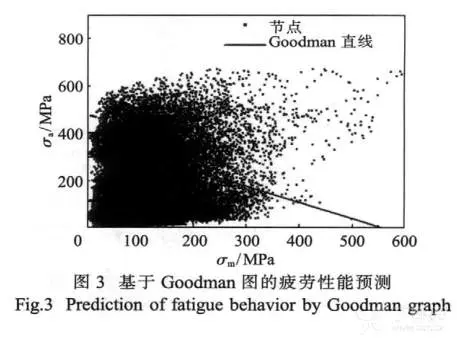
在最大应力为0.2的条件下,模型中很多点都落于危险区域,这说明在当下的条件下,支架很多位置都处于危险状态,多处会发生破坏。
1/FSF的分布图,如图4所示,破坏会发生在1/FSF的值大于1的位置。最大的1/FSF为2.05,位于近焊接点的圆弧处,这说明该点最有可能发生破坏。

2.2 直径对支架的影响
图 5 表示了在不同扩张直径下 , 支架的最大SEQA 和最大应变之间的关系。支架的直径增大时,支架模型的 SEQA 水平较低。随着拉伸应变的增加,最大 SEQA 也呈线性关系增大。
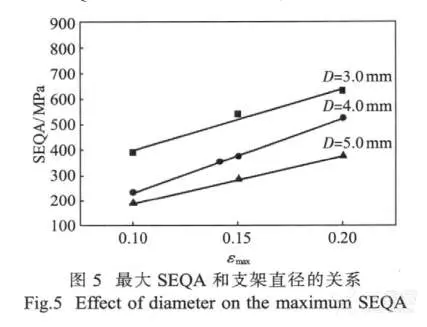
与此同时, 由 VonMises 应力所分析的结果由图 6 所示。
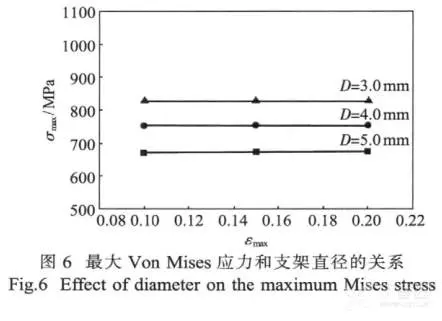
该结果和 SEQA 的结果完全相反,在较大直径下,模型有着较差的疲劳表现。同时,在不同的应变条件下, 模型的最大 Mises 应力并没有出现变化。考虑到疲劳周期下复杂的应力状况, VonMises 应力并不能正确反应支架的受力状况。
3 讨论
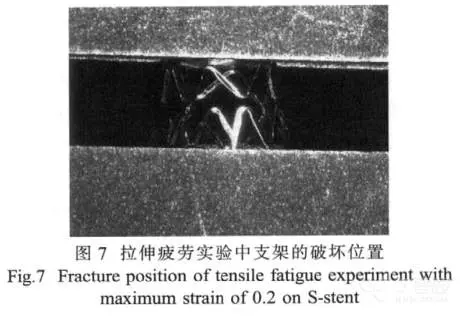
1/FSF 结果表明最危险的部位位于接近焊接点的圆弧处。与此同时,我们也进行了支架的拉伸疲劳实验,实际断裂位置 ( 图 7) 和 1/FSF 结果一致。这也再次证明了本研究模拟过程的有效性。
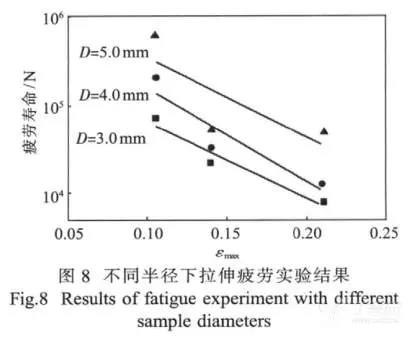
在不同直径下支架的疲劳拉伸实验结果由图 8所示。结果表明,较大直径的支架具有较长的疲劳寿命,这也证明了由 SEQA 计算的模拟结果。
4 结论
(1) 描述了支架在疲劳拉伸条件下的应力状况。关于疲劳表现, 在最大应变 0.2 的情况下,Goodman 图预测了模型多处将会发生疲劳断裂。
(2) 1/FSF 的分布图指出了最容易发生破坏的位置在支架近焊接点的圆弧处, 这点被拉伸疲劳实验所证明。关于半径对支架拉伸疲劳性能的影响,随着半径的增大,支架拉伸疲劳性能也会增大。同时,实验结果证明了在模拟过程中等效应力 SEQA 比 Mises 应力更能有效描述支架的受力状态。

