By: Tao Steven Zheng (郑涛)

【Problem】

The harmonic series is an infinite series given by the sum of reciprocals.

Part 1: Use the comparison test to prove that the harmonic series is divergent.

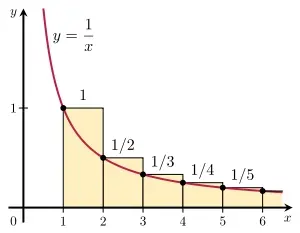
Part 2: Use the integral test to prove that the harmonic series is divergent.

【Solution】

Part 1: Comparison Test

Group the terms in the Harmonic series as follows:

It can be shown that each bracket grouped above is always greater than :

Therefore,

Since

it follows that

Part 2: Integral Test

Therefore,

【Historical Note】

This result in Part 1 (using the comparison test) was a proof by the Medieval French theologian, philosopher, and mathematician Nicole Oresme (c. 1325 - 1382 AD).