大偏差与统计力学

大偏差理论,从数学上来说是:
概率的指数递减的估计;
LLN与CLT的推广;
鞍点近似;
从物理上来说是:
熵与自由能的计算;
鞍点近似;
统计力学的数学基础(相当于微分几何与广义相对论的关系);
解释了统计力学中的各种最大原理的来源;
它在物理中提到的不多,但是实际上很早就在物理中用到(自由能,作用量等等,本质上都来自于此)。本文讨论基本的大偏差原理以及它在平衡态/非平衡态统计力学中的应用。

首先,什么叫做大偏差?我们称一族随机变量序列$\{A_n\}_{n=1}^\infty$满足LDP,若

Remark:
左边的da形式地表示[a,a+da]这个区间;
约等于号严格定义为两边取对数之后除以n的极限相等;
P(A_n\in da)这种表达是为了方便统一离散和连续的随机变量。如果是离散的,P(A_n\in da)就是一个数;如果是连续的,P(A_n\in da)=p_{A_n}(a)da表示概率密度函数。所以形式地这么写是比较舒服的,不用管测度、Radon-Nikodym导数之类的事情。当然一般当成连续的也没什么关系。
从物理上这样一个LDP表达式的意义。我们看A_n(典型的例子,比如说可以是iid的样本均值)的渐进形态:首先固定n,观察a的变动,I(a)(速率函数)相当于一个“energy landscape”(-I(a)可以理解为熵。I(a)总是非负的凸函数,可以有某些零点。而landscape的观点在扩散过程的平稳分布上更加直观);再把n变动,n表示体系的“大小”(比如化学反应系统的体积)。随着指标n的上升,从微观变成宏观,只有I(a)零点处的概率保留下来(LLN),远离零点的概率都指数下降至0(并且关于n是一阶的),也就是只剩下宏观统计性质。如果更细致地考察,把I(a)在零点处展开到二阶(一阶为0),则是一个正态分布,表示CLT。
所以LDP相当于LLN与CLT的推广,特别是在远离LLN处的微小概率的刻画(“大偏差”)。
物理上,速率函数(的相反数)代表熵,scaled cumulant generating function代表自由能。

大偏差这个toolbox要解决的就是两个问题:
对于某个r.v.列,建立起LDP;
计算出速率函数。
大偏差中最重要的三个定理:Gartner-Ellis定理,Varadhan定理,以及收缩原理,用于解决以上的两个问题。
首先是Gartner-Ellis定理。对于一个r.v.列\{A_n\},计算它的scaled cumulant generating function(一种母函数,物理上来说就是自由能):

如果它在R上存在并可微,那么这个序列就满足LDP。此时这个scaled cumulant generating function具有比较好的性质(0为一个零点,0处的各阶导数有比较明确的意义,凸函数)。进一步,对于第二个问题,速率函数就是scaled cumulant generating function的凸共轭。于是两个问题都完全解决了。
Varadhan定理。说的是跟Gartner-Ellis定理相反,scaled cumulant generating function是速率函数的凸共轭。
收缩原理。说的是r.v.的变换。如果A_n的速率函数为I_A(a),那么B_n=h(A_n)的速率函数为

这很好理解,只有概率最大(速率函数最小)的那个点被保留下来。大偏差理论中总是只有概率最大的那个点留下来(最大熵,最小作用量,带有三个inf的活化能)。

下面来看一些简单的应用。
把Gartner-Ellis定理用于iid序列的样本均值,得到的特例就是Cramer定理,此时scaled cumulant generating function退化为普通的cumulant generating function,直接经过一次Legendre-Fenchel变换就可以得到速率函数。下面拿指数分布的独立和来看看。考虑均值为1的iid指数分布列的样本均值A_n=\frac{X_1+\cdots+X_n}{n}。利用Gartner-Ellis定理容易计算出

这个速率函数的样子是(从landscape的角度看,可以直观地看出这个分布是偏向于右侧的)
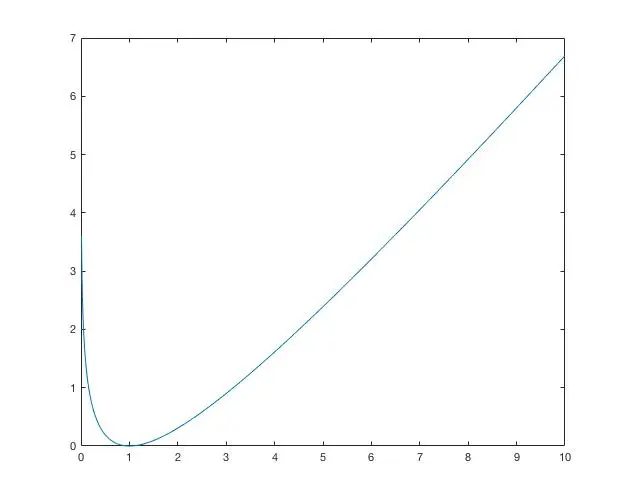
它的唯一零点为1,在1处的展开得到

这就是CLT,而且也可以看出随着n的增大,概率集中到1附近。但是这个展开在远离1的地方不成立,因为x比较大的时候速率函数是线性的,所以这实际上是一个长尾的分布,在大偏差的地方,CLT是无法正确刻画的(弱收敛当然还成立,但是分布函数的收敛是绝对的差趋于0,与此并不矛盾)。
接下来做一个数值模拟。生成100个指数分布的r.v.之样本均值的分布,观察其分布。需要比较的是Gartner-Ellis定理计算的结果与CLT给出的结果在对数坐标下的差别。

红线是CLT,绿线是速率函数。由图可见,速率函数(landscape)更加精确地刻画了远离均值的“大偏差”的分布,它与简单的CLT可能有数量级上的差别。这就是大偏差的意义所在。

接下来是LDP在数学上的进一步应用与扩展。前面(从大数定律出来的概率“凝聚”)iid样本均值的LDP(即Cramer定理)称为level-1的大偏差。
level-2的大偏差指的是Sanov定理意味上的。我们考虑经验测度(empirial measure)的问题。对于一个离散随机向量,我们可以定义一个新的随机向量L_n,称为“统计分布”或经验向量,表示“观察到的分布”。经验向量的分布也有LDP,因为从直观上来看,类似LLN,它的概率也应该凝聚到原有的分布向量附近。
直接应用(多元)的Gartner-Ellis定理,可以得到L_n的速率函数为(负的)相对熵,它仅在L_n的分布完全与原分布吻合时才为0,否则均为正数,所以经验向量的概率会指数地凝聚到这个点上。这称为Sanov定理,可以推广到连续r.v.。

关于Markov链的大偏差。它是iid序列的最简单的扩展,就像iid的SLLN可以推广到Markov链的遍历定理一样,我们可以把iid的LDP推广到Markov链,Cramer定理与Sanov定理都可以扩展,具体可以看Touchette的文章。

下面讨论速率函数非凸的情况,这一情况特别是在多稳态的时候会出现,此时Gartner-Ellis定理会失效,所以需要特别讨论。(待补足)

下面用大偏差理论建立平衡态统计力学。
大偏差与平衡态统计力学的联系在于:
速率函数~熵;
scaled cumulant generating function~自由能;
收缩原理~变分原理(热力学量的最大/最小化)。
下面是基本设定。
系统有n个“粒子”(可以是原子,分子,自旋,格点之类的对象),这个n就是随机变量列的指标,从小到大表示从微观到宏观,概率逐渐凝聚。
每个粒子的状态是一个随机变量\omega_i,总的概率空间的样本点是\omega=(\omega_1,\cdots,\omega_n),概率空间计为\Lambda_n。每个\omega在物理上也称作一个microstate,概率空间(加上sigma代数与概率测度)则可以称作一个系综。对一个系统,它处于某个随机的microstate。
这些粒子之间相互作用的Hamiltonian为一个随机变量H_n(\omega)(比如说Ising模型临近自旋的相互作用),平均能量定义为h_n(\omega)=H_n(\omega)/n,它被假设满足LDP(就像sampling mean),会逐渐凝聚到最大可能的值。
\Lambda_n上的先验的概率测度一般取为均匀测度。也有用别的先验概率的情况。具体看是什么系综。
所谓的macrostate或者说热力学量,就是指一个随机变量或者统计量M_n(\omega),它可以是温度等等。它应该要满足LDP,也就是说在热力学极限n\rightarrow \infty下,它的概率会凝聚于一个或若干个点,这就是“平衡态”统计物理。
这种设定从最微观开始就是随机的,并没有管从确定性动力学到随机的这一步,跟化学主方程的设定类似。至于最底层的是确定性还是随机,不管它。
统计力学就是找到热力学量,建立LDP,并计算速率函数。

下面考察平均能量的大偏差。这是统计物理中最基本的一个LDP。
假设平均能量h_n满足大偏差原理,则可以定义熵为速率函数的相反数

所以熵是能量u的函数。这里Boltzmann常数全部取为1,所以熵跟自由能都是无量纲量。换句话说,熵刻画了的是平均能量的分布情况:

所以熵最大也就意味着概率最大,在热力学极限下,只有熵最大的那个点留了下来。
自由能是按照scaled cumulant generating function定义的(稍微有些差别):

它是逆温度\beta的函数,也是一个无量纲量。\beta与u是一对共轭的变量。
需要注意的是这里的\phi跟热力学中的自由能可能差了一个\beta,它应该叫Massieu potential,不过方便起见就叫它自由能。
自由能与熵之间当然也就是Legendre-Fenchel变换的关系。
我们还可以定义配分函数(也是逆温度的函数)

它其实就是出现在自由能定义中的矩母函数。矩母函数包含了分布的完全信息,所以配分函数可以计算出各种物理学量,这在概率和统计力学上都是很对的。它的对数就是cumulant generating function。

微正则系综,即固定总能量H_n(\oemga)=U或h_n(\oemga)=u(当然粒子数n也是固定的)。概率测度定义为子流形上的均匀测度P^u。正则系综则为固定温度。二者都可以在前面的框架下考察(待补足)。

非平衡态统计力学,其数学形式已经不是随机变量,而是随机过程,即需要考虑含有时间的情况。基本的大偏差的思想如下:考察一条确定性的轨道

如果在这个轨道上加上恒定的微小的白噪声的随机扰动:

当\epsilon\rightarrow 0时,这样的轨道应该集中于确定性轨道周围。这样的一种概率上的“集中”或者说“凝聚”就是前面讨论的LDP。类比来想,这里的\frac{1}{\epsilon}就相当于前面的大偏差理论中的n,远离确定性轨道的概率应该是e^{-\frac{1}{\epsilon}c}方式递减的。这就是轨道大偏差的基本思想。
换句话说,随机变量的大偏差考虑的是“大体系极限(热力学极限)”下概率的凝聚,随机过程的大偏差考虑的是“弱噪声极限”下概率的凝聚。
对于轨道,比较麻烦的是难以定义随机函数的概率测度(当然是可以干的,即Kolmogorov扩展定理)。我们只考虑[o,\tau]这段有限长时间上的轨道X。形式地写一条轨道的“概率密度”P[X],它是一个泛函。Freidlin-Wentzell的理论指出

其中作用量泛函或者说熵为

L为Lagrangian。这一看就是一个路径积分的样子,作用量泛函只有在吻合确定性轨道的时候才为0,概率会凝结到这条轨道上。更一般地,如果扩散过程是一个一般的形式

那么拉格朗日量可以写成

其中A是扩散矩阵。此即扩散过程的Freidlin–Wentzell定理。在布朗运动的特殊情况,这称为Schilder定理。这样一个LDP的结果严格意义上应该怎么理解呢?
首先,J[x}是一个泛函,从C_0([0,\tau])映射到\bar{\mathbb{R}}上。如果X在Sobolev空间H^1([0,\tau])上的话,J[X]就按上面的方法定义;若不然(比如不可微),则定义为无穷大。对于每个C_0内的集合G,

所以无穷大并没有影响(体现的是收缩原理)。
接下来,考察从(0,x_0)跑到(\tau,x)的所有路径,它的大偏差为

其中的quasi-potential为

这其实就是WKB近似(\epsilon\rightarrow 0,其实就是\hbar\rightarrow 0,随机性消失,只剩下确定性)。这里面泛函的极小值问题就是经典的Lagrange力学问题,可以用Euler-Lagrange方程求解。WKB近似是把\hbar近似到1阶,轨道大偏差是把\epsilon近似到一阶,二者本质上是一回事。\hbar趋向于0时,量子力学也就退化为经典力学。这个近似其实也就是PDE(Fokker-Planck方程)的近似求解。
总的来说,轨道大偏差说的就是,有一些随机轨道,每条轨道都有不同的概率,各个轨道之间的概率分配是按照作用量泛函决定的,当随机性趋向于0时,只有其中概率最大的一条轨道被保留下来,概率都集中到它附近,其他轨道的概率都指数下降了。
如果联系量子力学的路径积分表示,还可以看到Feynman-Kac公式与Schrodinger方程的联系,Ito扩散过程的大偏差与路径积分的联系,这样概率论的两个方面与量子力学的两个方面都联系起来了。

Freidlin-Wentzell的轨道大偏差理论在数学中的应用,在下面会举出两个例子。

对于一个Ito扩散过程,我们经常讨论它在某一时刻的概率密度。严格的求解用的是Kolmogorov向前方程或者Fokker-Planck方程。但是在小噪声的极限下,Freidlin-Wentzell的轨道大偏差理论给出了一种近似求解某一时刻概率密度的方法,即用quasi-potential表示。这时候跟随机变量的大偏差类似,概率会集中在一个点附近。
考虑在一个有唯一稳定不动点的动力系统上加上弱小的噪声。最简单的情况为Ornstein-Uhlenbeck过程:

将其作用量最小化:

直接套用Euler-Langrange方程得到optimal path为

从而quasi-potential为

这正是平稳分布时的potential。


第二个问题是从吸引子处逃脱的问题。给定一个确定性动力学和一个稳定不动点,以及一个逃脱边界\partial D。逃脱边界内的确定性轨道全部会趋于稳定不动点,但加上噪声之后则有微小的概率在一定时间逃脱这个边界。定义逃脱时间

定义活化能

也就是把quasi-potential尽可能取到最小。那么Freidlin-Wentzell的理论严格证明了以下两个结果:

以及

这样一个活化能的形式被称为principle of minimum available energy,其实也是一种收缩原理,即“从最可能的时间和地点以最可能的路径逃出去”。
然后我们回到物理化学中的Arrhenius方程:

这看起来是一个Boltzmann分布的形式,以前也是按照这样理解的。但是,化学反应动力学是一个非平衡态,并没有所谓的Boltzmann分布。这里的速率,实际上可以理解为某种“逃脱时间”的倒数。那么根据前面的Freidlin-Wentzell理论,速率当然具有这种形式。所以,Freidlin-Wentzell理论解释了为什么自然界的动力学会有很多Arrhenius形式的规律。“活化能”的概念也是从这里来的。
最后的评述:这个结果实际上相当于Dynkin方程的WKB近似。

下面做一些数值模拟来验证上面的结果。考虑在势场

中的(弱)随机游动,考察其多久会逃出这个势阱。我们把它当作一个化学反应动力学的模型。SDE为

逃脱的边界为\pm 1。这个例子中的活化能无法解析求解,只能数值计算。我们略过这一步,直接用随机模拟来看<\tau_\epsilon>与\epsilon的关系。用Euler-Maruyama算法模拟随机轨道。数值模拟结果为

可见这是一条非常好的直线。拟合得到活化能为1.9591。顺带一提,从图中可以看到,随着活化能(这里指E/\epsilon)增大,时间是指数上升的,这是蛋白质折叠的Levinthal悖论的一个解释。

最后,关于最小作用量原理、程函、路径积分的一些评述。
熵和作用量本质上来说是一回事,都是某种分布的rate function。区别在于,熵是平衡态统计力学体系的某种热力学量(作为随机变量)的rate function,是一个名副其实的函数;而作用量则是某条轨道的泛函,是轨道分布的rate function。在热力学极限或者弱扰动极限/经典极限下,前者留下的只有熵最大的一个值,后者留下的只有作用量最小的一条轨道。所以说,最小作用量原理和最大熵原理是一回事。
在经典力学中,每条路径有一个作用量泛函,Euler-Langrange方程限制了确定性的轨道必然按照作用量泛函最小的那条轨道走。
在量子力学的路径积分表述中,轨道并不只有一条,每条轨道的概率与作用量泛函有关。在\hbar趋于0的经典极限下,就退回到Euler-Lagrange方程。把Schrodinger方程近似到\hbar的一阶,就是WKB近似,也就是轨道大偏差,此时大部分概率集中在optimal path附近。
在光学中,光程函就是作用量泛函即rate function。波动光学在波长趋于0的情况下,就有大偏差原理,近似为最小光程函附近的轨道(Fermat原理),从而就有Snell折射定律等等。

